题目内容
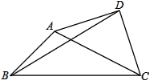
【题目】已知△ABC中,∠ABC=45°,AB=7![]() ,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为___.
【答案】![]()
【解析】
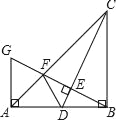
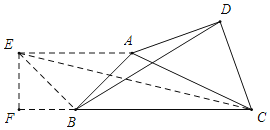
显然直接求BD不好入手,那么就将问题进行转化.注意到△ACD为等腰Rt△,于是以AB为腰向左作等腰Rt△ABE,则易证△ABD与△AEC相似,相似比为![]() ,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
,从而只需求出EC即可,此时∠EBC=135°,于是过E作EF⊥BC于F,则△EFB也为等腰Rt△,算出EF、BF,进而算出EC,问题迎刃而解.
以AB为腰作等腰Rt△ABE,连接EC,
∵△ADC为等腰Rt△,
∴![]() ,∠EAB=∠DAC=45°,
,∠EAB=∠DAC=45°,
∴∠EAB+∠BAC=∠BAC+∠DAC,
∴∠EAC=∠DAB,
∴△EAC∽△BAD,
∴![]() ,
,
作EF⊥BC交BC延长线于F,
∵∠ABC=45°,∠EBA=90°,
∴∠EBF=45°,
∴△EFB为等腰Rt△,
∴EF=FB=![]() EB=
EB=![]() AB=7,
AB=7,
∴EC=![]() =25,
=25,
∴BD=![]() EC=
EC=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
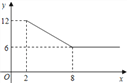
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
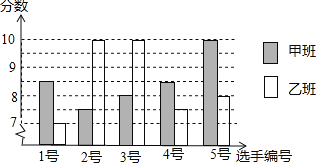
![]() 根据上图填写下表:
根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 |
|
| ______ | ______ |
乙班 |
| ______ | 10 |
|
![]() 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.