题目内容
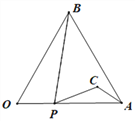
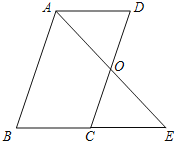
【题目】已知:如图,□ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
![]() 求证:
求证: ![]() ≌
≌![]() ;
;
![]() 连接
连接![]() ,当
,当![]() ______°和
______°和![]() ______°时,四边形ACED是正方形?请说明理由.
______°时,四边形ACED是正方形?请说明理由.
【答案】 45 45
【解析】分析:
(1)由已知条件易得∠D=∠OCE,DO=CO,∠AOD=∠COE,由此即可证得△AOD≌△EOC;
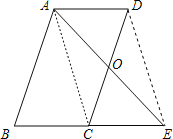
(2)如下图,由△AOD≌△EOC可得AO=EO,DO=BO,从而可得四边形ACED是平行四边形,结合四边形ABCD是平行四边形可得AD=BC=CE,此时要使四边形ACED是正方形,则需∠ACE=90°,AE=CE,故只需∠B=∠AEB=45°即可得到∠BAE=90°,结合BC=CE即可得到所需结论,从而得到四边形ACED是正方形.
详解:
(1)∵点O是CD的中点,
∴DO=CO,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在![]() 和
和![]() 中
中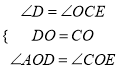 ,
,
∴![]() ≌
≌![]() ;
;
![]() 当
当![]() 和
和![]() 时,四边形ACED是正方形,
时,四边形ACED是正方形,
∵![]() 和
和![]() ,
,
∴![]() ,
,
∵![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形ACED是平行四边形,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴平行四边形ACED是菱形,
∵![]() ,
,
∴![]() ,
,
∴四边形ACED是正方形.
故答案为: ![]() .
.

练习册系列答案
相关题目