题目内容
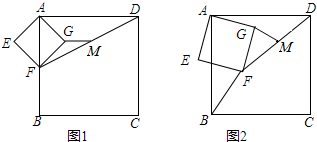
1.已知正方形ABCD和正方形AEFG,点F在边AB上,点M为DF的中点,连GM.(1)在图1中画出△AEF绕A点逆时针旋转90°后的图形;
(2)在图1中,求证:BF=2MG;
(3)将图1中的正方形AEFG绕A点逆时针旋转至图2的位置,其他条件不变,问(2)中的结论是否仍然成立,若成立请证明,若不成立说明理由.
分析 (1)根据旋转变换的性质和正方形的性质作图即可;
(2)根据旋转的性质得到AF′=AF,得到DF′=BF,根据三角形中位线定理得到GM=$\frac{1}{2}$DF′,从而证明结论;
(3)把四边形AEFG绕A点逆时针旋转90°得到四边形AGF′G′,根据旋转的性质和三角形中位线定理证明即可.
解答 解:(1)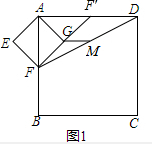 如图1,△AGF′即为所求;
如图1,△AGF′即为所求;
(2)证明:由题意得,AF′=AF,又AB=AD,
∴DF′=BF,
∵∠FAG=45°,∠BAD=90°,
∴∠FAG=∠F′AG,又AF′=AF,
∴G是FF′的中点,又M为DF的中点,
∴GM=$\frac{1}{2}$DF′,
∴BF=2MG;
(3)(2)中的结论仍然成立.
证明: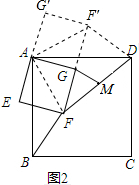 把四边形AEFG绕A点逆时针旋转90°得到四边形AGF′G′,
把四边形AEFG绕A点逆时针旋转90°得到四边形AGF′G′,
则G是FF′的中点,又M为DF的中点,
∴GM=$\frac{1}{2}$DF′,
由旋转的性质可得,△ADF′≌△ABF,
∴DF′=BF,
∴BF=2MG.
点评 本题考查的是正方形的性质、旋转变换的性质,掌握正方形的四条边相等、四个角都是直角是解题的关键,注意旋转变换中的旋转角、旋转方向和旋转中心要把握准确.

练习册系列答案
相关题目
11.满足下列条件的△ABC,不是直角三角形的是( )
| A. | ∠A:∠B:∠C=3:4:5 | B. | ∠A-∠B=∠C | C. | a2-b2=c2 | D. | a:b:c=7:24:25 |
13.若整数k满足k<$\sqrt{90}$<k+1,则k的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |

 如图,已知直线l:y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴交于点A,与y轴交于点B,将△AOB沿直线l折叠,点O落在点C处,求直线CA的表达式.
如图,已知直线l:y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴交于点A,与y轴交于点B,将△AOB沿直线l折叠,点O落在点C处,求直线CA的表达式.