题目内容
2.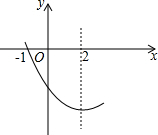 抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(-3,y1)(-6,y2)都在抛物线上,则y1<y2.其中正确的是①③④⑤.(只填序号)
抛物线y=ax2+bx+c(a≠0)图象的一部分如图所示,其对称轴为x=2,与x轴的一个交点是(-1,0),有以下结论:①abc>0;②4a-2b+c<0;③4a+b=0④抛物线与x轴的另一个交点是(5,0)⑤若点(-3,y1)(-6,y2)都在抛物线上,则y1<y2.其中正确的是①③④⑤.(只填序号)
分析 ①先确定a、b、c的符号,再确定abc的符号;
②根据当x=-2时,y的符号来确定4a-2b+c的符号;
③根据对称轴:x=-$\frac{b}{2a}$=2,化简得出;
④由对称性得出结论;
⑤利用增减性得出y1和y2的大小.
解答 解:①∵抛物线开口向下,
∴a<0,
∵对称轴是:x=2,
∴a、b异号,
∴b>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,
∴选项①正确;
②由图象得:当x=-2时,y>0,
∴4a-2b+c>0,
∴选项②不正确;
③抛物线对称轴是:x=-$\frac{b}{2a}$=2,
b=-4a,
4a+b=0,
∴选项③正确;
④由对称性得:抛物线与x轴的另一个交点为(5,0),
∴选项④正确;
⑤∵对称轴是:x=2,且开口向上,
∴当x<2时,y随x的增大而减小,
∵-3>-6,
∴y1<y2,
∴选项⑤正确;
故答案为:①③④⑤.
点评 本题考查了抛物线与x轴的交点、二次函数的图象与系数的关系以及二次函数的性质、抛物线的单调性、对称性等问题;灵活运用有关知识来分析、解答是关键.

练习册系列答案
相关题目
13.统计小强5次射击的成绩如下:(单位:环)5,9,7,10,9.其方差为3.2,如果他再射击1次,命中8环,那么他的射击成绩的方差( )
| A. | 变大 | B. | 变小 | C. | 不变 | D. | 无法确定 |
7.估计$\frac{\sqrt{3}+3}{2}$的值在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
14.为了筹备毕业联欢会,班委会对全班同学爱吃哪几种水果作了民意调查,并进行数据整理,在设计买水果的方案时,下面的调查数据中最值得关注的是( )
| A. | 平均数 | B. | 加权平均数 | C. | 中位数 | D. | 众数 |
12.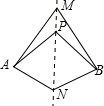 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | ∠ANM=∠BNM | C. | ∠MAP=∠MBP | D. | AP=BN |
 ,当输出的数是10时,输入时的x=8.
,当输出的数是10时,输入时的x=8. 如图,四边形ABCD内接于⊙O,若∠BAD=110°,则∠C的度数是70°.
如图,四边形ABCD内接于⊙O,若∠BAD=110°,则∠C的度数是70°.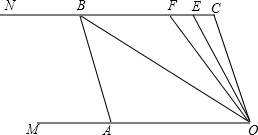 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,点F在线段CB上,OB平分∠AOF,OE平分∠COF.
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,点F在线段CB上,OB平分∠AOF,OE平分∠COF.