题目内容
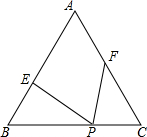 已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为4 时,求x的值.②四边形AEPF的面积是否存在最大值?若存在,请直接写出面积的最大值;若不存在,请说明理由.
时,求x的值.②四边形AEPF的面积是否存在最大值?若存在,请直接写出面积的最大值;若不存在,请说明理由.
解:(1)∵∠EPF=60°,
∴∠BPE+∠CPF=120°,
∵等边三角形ABC,
∴∠B=60°,
∴∠BPE+∠BEP=120°,
∴∠BEP=∠CPF,
∵∠B=∠C=60°,
∴△BEP∽△CPF,
∴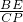 =
=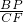 ,
,
∴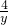 =
= ,
,
∴y= ;
;
∵当F和A重合时,y=CF=6,x= ,
,
即x的取值范围是 ≤x≤6;
≤x≤6;
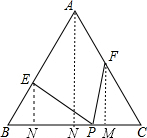 (2)①过A作AD⊥BC于D,
(2)①过A作AD⊥BC于D,
过E作EN⊥BC于N,过F作FM⊥BC于M,
∵∠B=60°,AB=6,BE=x,
∴AD=sin60°×6=3 ,EN=sin60°×x=
,EN=sin60°×x= x,
x,
∵∠C=60°,CF=y= ,
,
∴FM=sin60°× =
= ,
,
∴S四边形AEPF=S△ABC-S△BEP-S△CFP= ×6×3
×6×3 -
- ×4×
×4× x-
x- ×2×
×2× =9
=9 -
- x-
x- =4
=4 ,
,
x2-5x+4=0,
x=1(舍去),x=4,
∴当四边形AEPF的面积为4 时,x=4;
时,x=4;
②四边形AEPF的面积存在最大值,
9 -
- x-
x- =-
=- (
( +x-9)=-
+x-9)=- [(
[(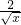 -
- )2-5]=-
)2-5]=- (
(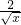 -
- )2+5
)2+5
即最大值是5 .
.
分析:(1)求出△BEP∽△CPF,得出比例式,代入求出即可;
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,求出AD=3 ,EN=
,EN= x,CF=y=
x,CF=y= ,FM=
,FM= ,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
②四边形AEPF的面积存在最大值,把9 -
- x-
x- 化成-
化成- (
(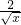 -
- )2+5
)2+5 ,即可得出答案.
,即可得出答案.
点评:本题考查了解直角三角形,等边三角形性质,相似三角形的性质和判定,三角形的面积,勾股定理,函数的最值等知识点的应用,题目综合性比较强,难度偏大.

∴∠BPE+∠CPF=120°,
∵等边三角形ABC,
∴∠B=60°,
∴∠BPE+∠BEP=120°,
∴∠BEP=∠CPF,
∵∠B=∠C=60°,
∴△BEP∽△CPF,
∴
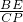 =
=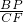 ,
,∴
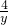 =
= ,
,∴y=
 ;
;∵当F和A重合时,y=CF=6,x=
 ,
,即x的取值范围是
 ≤x≤6;
≤x≤6; (2)①过A作AD⊥BC于D,
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,
∵∠B=60°,AB=6,BE=x,
∴AD=sin60°×6=3
 ,EN=sin60°×x=
,EN=sin60°×x= x,
x,∵∠C=60°,CF=y=
 ,
,∴FM=sin60°×
 =
= ,
,∴S四边形AEPF=S△ABC-S△BEP-S△CFP=
 ×6×3
×6×3 -
- ×4×
×4× x-
x- ×2×
×2× =9
=9 -
- x-
x- =4
=4 ,
,x2-5x+4=0,
x=1(舍去),x=4,
∴当四边形AEPF的面积为4
 时,x=4;
时,x=4;②四边形AEPF的面积存在最大值,
9
 -
- x-
x- =-
=- (
( +x-9)=-
+x-9)=- [(
[(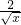 -
- )2-5]=-
)2-5]=- (
(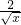 -
- )2+5
)2+5
即最大值是5
 .
.分析:(1)求出△BEP∽△CPF,得出比例式,代入求出即可;
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,求出AD=3
 ,EN=
,EN= x,CF=y=
x,CF=y= ,FM=
,FM= ,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;②四边形AEPF的面积存在最大值,把9
 -
- x-
x- 化成-
化成- (
(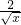 -
- )2+5
)2+5 ,即可得出答案.
,即可得出答案.点评:本题考查了解直角三角形,等边三角形性质,相似三角形的性质和判定,三角形的面积,勾股定理,函数的最值等知识点的应用,题目综合性比较强,难度偏大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知等边△ABC,以边BC为直径的半圆与边AB,AC分别交于点D、E,过点D作DF⊥AC于点F,
如图,已知等边△ABC,以边BC为直径的半圆与边AB,AC分别交于点D、E,过点D作DF⊥AC于点F,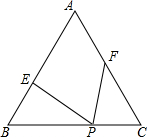 (2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.