题目内容
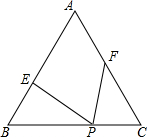 (2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为4
| 3 |
分析:(1)求出△BEP∽△CPF,得出比例式,代入求出即可;
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,求出AD=3
,EN=
x,CF=y=
,FM=
,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
②四边形AEPF的面积存在最大值,把9
-
x-
化成-
(
-
)2+5
,即可得出答案.
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,求出AD=3
| 3 |
| ||
| 2 |
| 8 |
| x |
4
| ||
| x |
②四边形AEPF的面积存在最大值,把9
| 3 |
| 3 |
4
| ||
| x |
| 3 |
| 2 | ||
|
| x |
| 3 |
解答:解:(1)∵∠EPF=60°,
∴∠BPE+∠CPF=120°,
∵等边三角形ABC,
∴∠B=60°,
∴∠BPE+∠BEP=120°,
∴∠BEP=∠CPF,
∵∠B=∠C=60°,
∴△BEP∽△CPF,
∴
=
,
∴
=
,
∴y=
;
∵当F和A重合时,y=CF=6,x=
,
即x的取值范围是
≤x≤6;
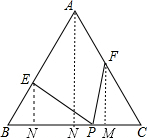 (2)①过A作AD⊥BC于D,
(2)①过A作AD⊥BC于D,
过E作EN⊥BC于N,过F作FM⊥BC于M,
∵∠B=60°,AB=6,BE=x,
∴AD=sin60°×6=3
,EN=sin60°×x=
x,
∵∠C=60°,CF=y=
,
∴FM=sin60°×
=
,
∴S四边形AEPF=S△ABC-S△BEP-S△CFP=
×6×3
-
×4×
x-
×2×
=9
-
x-
=4
,
x2-5x+4=0,
x=1(舍去),x=4,
∴当四边形AEPF的面积为4
时,x=4;
②四边形AEPF的面积存在最大值,
9
-
x-
=-
(
+x-9)=-
[(
-
)2-5]=-
(
-
)2+5
即最大值是5
.

∴∠BPE+∠CPF=120°,
∵等边三角形ABC,
∴∠B=60°,
∴∠BPE+∠BEP=120°,
∴∠BEP=∠CPF,
∵∠B=∠C=60°,
∴△BEP∽△CPF,
∴
| BE |
| CP |
| BP |
| CF |
∴
| 4 |
| y |
| x |
| 6-4 |
∴y=
| 8 |
| x |
∵当F和A重合时,y=CF=6,x=
| 4 |
| 3 |
即x的取值范围是
| 4 |
| 3 |
 (2)①过A作AD⊥BC于D,
(2)①过A作AD⊥BC于D,过E作EN⊥BC于N,过F作FM⊥BC于M,
∵∠B=60°,AB=6,BE=x,
∴AD=sin60°×6=3
| 3 |
| ||
| 2 |
∵∠C=60°,CF=y=
| 8 |
| x |
∴FM=sin60°×
| 8 |
| x |
4
| ||
| x |
∴S四边形AEPF=S△ABC-S△BEP-S△CFP=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
4
| ||
| x |
| 3 |
| 3 |
4
| ||
| x |
| 3 |
x2-5x+4=0,
x=1(舍去),x=4,
∴当四边形AEPF的面积为4
| 3 |
②四边形AEPF的面积存在最大值,
9
| 3 |
| 3 |
4
| ||
| x |
| 3 |
| 4 |
| x |
| 3 |
| 2 | ||
|
| x |
| 3 |
| 2 | ||
|
| x |
| 3 |
即最大值是5
| 3 |
点评:本题考查了解直角三角形,等边三角形性质,相似三角形的性质和判定,三角形的面积,勾股定理,函数的最值等知识点的应用,题目综合性比较强,难度偏大.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (2013•海门市一模)小张到老王的果园里一次性采购一种水果,他俩商定:小张的采购价y (元/吨)与采购x (吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).
(2013•海门市一模)小张到老王的果园里一次性采购一种水果,他俩商定:小张的采购价y (元/吨)与采购x (吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C).