题目内容
已知等边△ABC外有一点P,设P到BC、CA、AB的距离分别为h1,h2,h3,且h1-h2+h3=6,那么等边△ABC的面积为分析:根据等边三角形的面积即可计算(h1-h2+h3)是等边三角形ABC的高,根据等边三角形的高即可求得BC的值,即可求得△ABC的面积,即可解题.
解答: 解:设等边△ABC的边长为a,连接PA、PB、PC,
解:设等边△ABC的边长为a,连接PA、PB、PC,
则S△PAB+S△PBC-S△PAC=S△ABC,
从而
ah1-
ah2+
ah3=
a2,
即
a(h1-h2+h3)=
a2,
∵h1-h2+h3=6,
∴a=4
,
∴S△ABC=
a2=12
.
故答案为12
.
 解:设等边△ABC的边长为a,连接PA、PB、PC,
解:设等边△ABC的边长为a,连接PA、PB、PC,则S△PAB+S△PBC-S△PAC=S△ABC,
从而
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
即
| 1 |
| 2 |
| ||
| 4 |
∵h1-h2+h3=6,
∴a=4
| 3 |
∴S△ABC=
| ||
| 4 |
| 3 |
故答案为12
| 3 |
点评:本题主要考查了等边三角形面积的计算,等边三角形高线长与边长的关系,本题中根据等边三角形的高计算等边三角形的面积是解题的关键.

练习册系列答案
相关题目
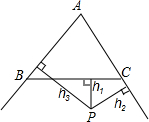 如图,已知等边△ABC外有一点P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3-h1=6,那么等边△ABC的面积为( )
如图,已知等边△ABC外有一点P,P落在∠ABC内,设点P到BC、CA、AB三边的距离分别为h1、h2、h3,且满足h2+h3-h1=6,那么等边△ABC的面积为( )



