题目内容
10．甲卖橘子x千克与所获利润y（元）满足关系式y=-x2+120x-1200，则当甲卖出60千克橘子时，获得最大利润为2400元．分析 根据配方法把二次函数的一般式化为顶点式，根据二次函数的性质确定函数的对称轴和最大值．
解答 解：y=-x2+120x-1200=-（x-60）2+2400，
∵-1＜0，∴函数有最大值，
当x=60时，函数有最大值2400，
故答案为：60；2400．
点评 本题考查的是二次函数的最值的求法，掌握二次函数的性质和配方法是解题的关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
20．有这样一组数：1，2，3，5…现以这组数据的数作为正方形边长的长度构造如图正方形；再分别从左到右取2个，3个，4个，5个正方形拼成如下长方形记为：①②③（如图所示），则第⑨个长方形的周长是288
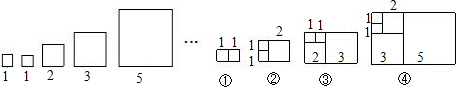
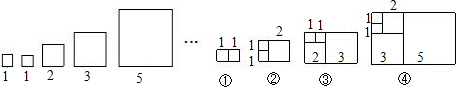
18．计算|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{3}$-2|+|2-$\sqrt{5}$|+…+|$\sqrt{2013}$-$\sqrt{2014}$|的结果是（ ）
| A． | $\sqrt{2013}$-1 | B． | $\sqrt{2014}$-1 | C． | 1-$\sqrt{2013}$ | D． | 1-$\sqrt{2014}$ |
如图所示是长方形养鸡场平面示意图，一面靠墙，且墙长为18米，另外三面用竹篱笆围成，若竹篱笆总长为35m，围的面积为150m2，则此长方形鸡场的长、宽分别为15米、10米．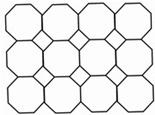
如图是以正八边形为“基本单位”铺成的图案的一部分，（其中有4×3个“基本单位”），其间存有若干个小正方形空隙，以及图案的4个角处有更小的三角形空隙，若密铺5×4个“基本单位”的图案，并填满空隙，则需要12个小正方形，14小三角形．（不含图案的4个角）