题目内容
如图①,已知抛物线C1: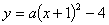 的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1)求点C的坐标及 a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3.C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
 |  | ||
解:(1)顶点C为(-1,-4) ………………………………………1分
∵点B(1,0)在抛物线C1上,∴ ,解得,a=1 ………2分
,解得,a=1 ………2分
(2)①∵C2与C1关于x轴对称,∴抛物线C2的表达式为 ……3分
……3分
抛物线C3由C2平移得到,∴抛物线C3为 ……4分
……4分
∴E(5,0)
设直线CE的解析式为:y=kx+b,
则 ,解得
,解得 ,…………………………………………………5分
,…………………………………………………5分
∴直线BC的解析式为y= x﹣
x﹣ , …………………………………………………6分
, …………………………………………………6分
设P(x,﹣x2+6x﹣5),则F(x, x﹣
x﹣ ),
),
∴PF=(﹣x2+6x﹣5)﹣( x﹣
x﹣ )=﹣x2+
)=﹣x2+ x﹣
x﹣ =﹣(x﹣
=﹣(x﹣ )2+
)2+ ,………8分
,………8分
∴当x= 时,PF有最大值为
时,PF有最大值为 .…………………………………………………9分
.…………………………………………………9分
②若PE=EF,∵ PF⊥x轴,∴x轴平分PF,
∴﹣x2+6x﹣5=- x+
x+ , …………………………………………………10分
, …………………………………………………10分
解得x1= ,x2=5(舍去)
,x2=5(舍去)
∴P( ,
, ).
).

练习册系列答案
相关题目
 B.
B.
 D.
D.

 等的圆是等圆; ②长度相等弧是等弧; ③一个圆只有一条直径 ;④直径是圆中最长的弦.其中正确的个数是……………………………………
等的圆是等圆; ②长度相等弧是等弧; ③一个圆只有一条直径 ;④直径是圆中最长的弦.其中正确的个数是…………………………………… ……( )
……( )

 角平分线于点F.求证:EA=EF.
角平分线于点F.求证:EA=EF.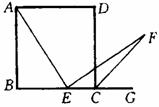
 AB; ③AB=2AP; ④AP+PB=AB。
AB; ③AB=2AP; ④AP+PB=AB。