题目内容
【发现】
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
【思考】
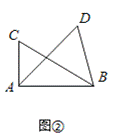
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
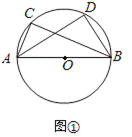

小明尝试用反证法:如图③,过A、B、C三点作圆,圆心为O,假设点D在圆O外,设AD交圆O于点E,连接BE,则∠AEB=∠ACB,又由∠AEB是△BDE的一个外角,得∠AEB>∠ADB,因此∠ACB>∠ADB,就与条件∠ACB=∠ADB相矛盾,所以点D不在圆O外。
点D可能在⊙O内吗?,请你补全小明的解题过程(画出示意图)并给出你的结论。
【应用】
利用【发现】和【思考】中的结论解决问题:
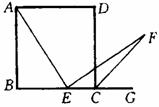
(1)如图④,四边形ABCD是正方形,点E为BC上的任一点,AE⊥EF,EF交∠BCD的外 角平分线于点F.求证:EA=EF.
角平分线于点F.求证:EA=EF.
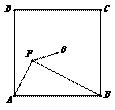
(2)如图⑤,正方形ABCD的中心为O,面积为1989cm2.P为正方形内一点,且∠OPB=45°,PA:PB=5:14.求OP长度
图④ 图⑤
解:【思考】如图1,假设点D在⊙O内,延长AD交⊙O于点E,连接BE,则∠AEB=∠ACB,
∵∠ADE是△BDE的外角,
∴∠ADB>∠AEB,
∴∠ADB>∠ACB,
因此,∠ADB>∠ACB这与条件∠ACB=∠ADB矛盾,------------2分
所以点D也不在⊙O内,
所以点D即不在⊙O内,也不在⊙O外,点D在⊙O上;------------3分
【应用】
(1)连接AC AF------------4分
∵正方形ABCD
∴∠ACB=∠ACD=45° ∠DCG=90°
∵CF平分∠DCG
∴ ∠DCF=45°
∴ ∠ACF=90°
 ∵ ∠AEF=∠ACF=90°
∵ ∠AEF=∠ACF=90°
∴ A,E,C,F四点共圆------------6分
∴ ∠AFE=∠ACB=45°
∴ EA=EF------------7分
(2)如图连接OA,OB,
∵正方形ABCD的中心为O,∠OPB=45°,
∴∠OAB=∠OPB=45°,∠OBA=45°,OA=OB
∴O,P,A,B四点共圆, ------------8分
∴∠APB=∠AOB=180°-45°-45°=90°,
在△PAB中由勾股定理得:PA2+PB2=AB2=1989,
由于PA:PB=5:14,
设PA=5x,PB=14x,
(5x)2+(14x)2=1989,
解得:x=3,
∴PB=14x=42.------------10分
作OE⊥OP交PB于点E
∴OP=OE
∵ ∠AOB=∠POE=90°
∴∠POA=∠EOB
∴△OPA≌△OEB
∴AP=BE=15
∴PE=PB-BE=27
∴OP=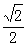 ×27=
×27=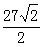 ------------12分
------------12分

如图,在 中,
中, cm,
cm, cm;动点
cm;动点 从点
从点 开始沿
开始沿 以
以 cm/s的速度向点
cm/s的速度向点 移动,动点
移动,动点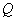 从点
从点 开始沿
开始沿 以4 cm/s的速度向点
以4 cm/s的速度向点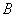 移动,动点
移动,动点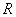 从点
从点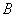 开始沿
开始沿 以 2cm/s的速度向点
以 2cm/s的速度向点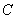 移动.如果
移动.如果 、
、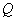 、
、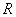 分别从
分别从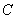 、
、 、
、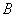 同时移动,移动时间为
同时移动,移动时间为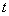
 s.
s.
(1) 的度数是 ;
的度数是 ;
(2)以 为直径的
为直径的 与
与 交于点
交于点 ,当
,当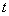 为何值时,
为何值时, 与
与 相切?
相切?
(3)写出 的面积
的面积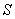 随动点移动时间
随动点移动时间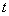 的函数关系式,并求
的函数关系式,并求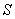 的最小值及相应的
的最小值及相应的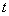 值;
值;
|
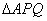 为等腰三角形,若存在,求出相应的
为等腰三角形,若存在,求出相应的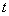 值,若不存在请说明理由.
值,若不存在请说明理由. 第28题图 备用图

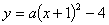 的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1. 



 0元,经市场预测,每个小家电的销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个小家电定价增加x元.
0元,经市场预测,每个小家电的销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个小家电定价增加x元. 写出售出一个小家电可获得的利润是多少元?(用含x的代数式表示);
写出售出一个小家电可获得的利润是多少元?(用含x的代数式表示); 000元,并且使进货量较少,则每个小家电的定价为多少元?
000元,并且使进货量较少,则每个小家电的定价为多少元? 的图象的顶点坐标是
的图象的顶点坐标是 B.
B. C.
C. D.
D.
