题目内容
1．过⊙O内一点N的最长弦为6，最短的弦长为4，那么ON的长为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{5}$ | D． | $\sqrt{3}$ |
分析 根据圆中的概念，首先应明确过一点圆中最长的弦是过这点的直径，最短的弦是垂直于这点和圆心的连线的弦，从而根据垂径定理和勾股定理进行计算．
解答 
解：如图所示，则直径AB是过点N的最长的弦．
过N点作弦CD⊥AB，则CD是过N的最短的弦．
连接OC．
∵ON⊥CD，
∴CN=$\frac{1}{2}$CD=2，
又OC=3，
∴ON=$\sqrt{5}$．
故选C．
点评 此题考查了垂径定理和勾股定理，难点在于弄清过圆内一点的最长的弦和最短的弦．
练习册系列答案
相关题目
13．某粮店出售的某品牌的面粉袋上标有质量为（25±0.1）㎏，它的质量最多相差（ ）
| A． | 0.8㎏ | B． | 0.6㎏ | C． | 0.2㎏ | D． | 0.4㎏ |
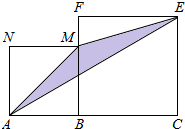如图，线段AC=n+1（其中n为正整数），点B在线段AC上，在线段AC同侧作正方形ABMN及正方形BCEF，连接AM、ME、EA得到△AME．当AB=1时，△AME的面积记为S1；当AB=2时，△AME的面积记为S2；当AB=3时，△AME的面积记为S3；…；当AB=n时，△AME的面积记为Sn，则Sn=$\frac{1}{2}$n2．（用含n的代数式表示）