题目内容
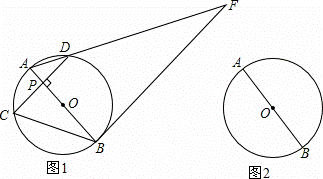
如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点 P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)若CD=2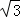 ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
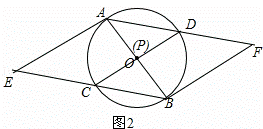
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
: (1)解:CD⊥AB,
∴PC=PD=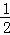 CD=
CD=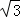 ,
,
连接OC,设⊙O的半径为r,则PO=PB﹣r=4﹣r,
在RT△POC中,OC2=OP2+PC2,
即r2=(4﹣r)2+(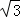 )2,解得r=
)2,解得r=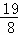 .
.
(2)证明:∵∠A=∠C,∠F=∠ABC,
∴ △PBC∽△BFA,
△PBC∽△BFA,
∴∠ABF=∠CPB,
∵CD⊥AB,
∴∠ABF=∠CPB=90°,
∴直线BF是⊙O的切线;
(3)四边形AEBF是平行四边形;
理由:解:如图2所示 :∵CD⊥AB,垂足为P,
:∵CD⊥AB,垂足为P,
∴当点P与点O重合时,CD=AB,
∴OC=OD,
∵AE是⊙O的切线,
∴BA⊥AE,
∵CD⊥AB,
∴DC∥AE,
∵AO=OB,
∴OC是△ABE的中位线,
∴AE=2OC,
∵∠D=∠ABC,∠F=∠ABC.
∴∠D=∠F,
∴CD∥BF,
∵AE∥BF,
∵OA=OB,
∴OD是△ABF的中位线,
∴BF=2OD,
∴AE=BF,
∴四边形AEBF是平行四边形.


练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目

 的值是
的值是 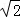 ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
 B.
B.  C.
C.  D.
D. 
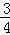 x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+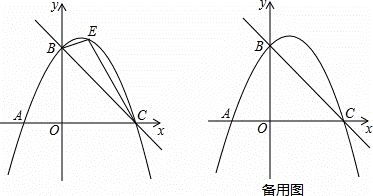
 于E,
于E, ,则
,则 _______。
_______。