题目内容
14. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )| A. | 10m | B. | 12m | C. | 12.4m | D. | 12.32m |
分析 根据题意得出△ABC∽△EDC,进而利用相似三角形的性质得出答案.
解答 解:由题意可得:AB=1.5m,BC=0.5m,DC=4m,
△ABC∽△EDC,
则$\frac{AB}{ED}$=$\frac{BC}{DC}$,
即$\frac{1.5}{DE}$=$\frac{0.5}{4}$,
解得:DE=12,
故选:B.
点评 此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.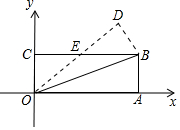 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )| A. | $y=\frac{4}{5}x$ | B. | $y=\frac{5}{4}x$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
9.中国人最早使用负数,可追溯到两千多年前的秦汉时期,-0.5的相反数是( )
| A. | 0.5 | B. | ±0.5 | C. | -0.5 | D. | 5 |
6.下列运算正确的是( )
| A. | (a2)m=a2m | B. | (2a)3=2a3 | C. | a3•a-5=a-15 | D. | a3÷a-5=a-2 |
5.若m>0,且m-$\frac{1}{m}$=3,则m+$\frac{1}{m}$等于( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{13}$ | D. | $\sqrt{11}$ |
6.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2+2x+1=x(x+2)+1 | C. | x2-2x=x(x-2) | D. | 4x2-6x=x(4x-6) |
 如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
如图,在Rt△ABC中,∠C=Rt∠,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.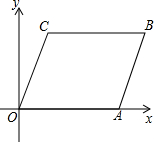 如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是(7,4).
如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是(7,4).