题目内容
14.在平面直角坐标系中,△ABC顶点B的坐标为(-2,1),若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比等于$\frac{1}{2}$,则点B′的坐标为(-4,2)或(4,-2).分析 位似是特殊的相似,若两个图形△ABC和△A′B′C′以原点为位似中心,相似比是k,△ABC上一点的坐标是(x,y),则在△A′B′C′中,它的对应点的坐标是(kx,ky)或(-kx,-ky).
解答 解:∵△ABC顶点B的坐标为(-2,1),以原点O为位似中心,使△ABC与△A′B′C′的相似比等于$\frac{1}{2}$,
∴B'的坐标为(-4,2)或(4,-2).
故答案为:(-4,2)或(4,-2).
点评 此题主要考查了位似变换,正确理解位似与相似的关系,记忆关于原点位似的两个图形对应点坐标之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列运算正确的是( )
| A. | x2x3=x6 | B. | x2+x2=2x4 | C. | (-2x)2=4x2 | D. | (-2x)2 (-3x)3=6x5 |
9.地球半径约为6 400 000米,这个数用科学记数法表示为( )
| A. | 640×104 | B. | 64×105 | C. | 6.4×106 | D. | 0.64×107 |
4.下列说法正确的是( )
| A. | 三点确定一个圆 | B. | 平分弦的直径垂直于弦 | ||
| C. | 等弧所对的圆周角相等 | D. | 垂直于半径的直线是圆的切线 |
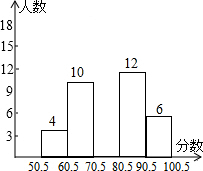 某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:
某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题: 如图,己知AB=8,以AB为斜边作Rt△ABC,∠ACB=90°,过点C作AB的平行线,再过点A作AB的垂线,使两线相交于点D.设AC=x,DC=y;则(x-y)的最大值是2.
如图,己知AB=8,以AB为斜边作Rt△ABC,∠ACB=90°,过点C作AB的平行线,再过点A作AB的垂线,使两线相交于点D.设AC=x,DC=y;则(x-y)的最大值是2.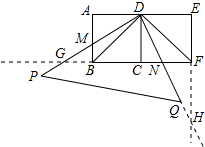 如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.