题目内容
 如图,在直角三角形纸片上进行如下设计,直角三角形的两直角边与展开图左下角的正方形边重合,斜边恰好经过两个正方形的顶点,已知BC=36,则这个展开图围成的正方体的棱长为
如图,在直角三角形纸片上进行如下设计,直角三角形的两直角边与展开图左下角的正方形边重合,斜边恰好经过两个正方形的顶点,已知BC=36,则这个展开图围成的正方体的棱长为
- A.

- B.
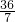
- C.6
- D.3
A
分析:如图,设正方体的棱长为x,则DE=x,FG=4x,根据相似三角形的性质可以用x表示出AD,再根据△AFG∽△ABC就可以求出正方体的棱长.
解答: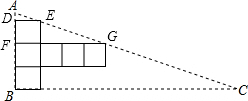 解:由题意可知△ADE∽△AFG,
解:由题意可知△ADE∽△AFG,
则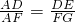 .
.
设正方体的棱长为x,则DE=x,FG=4x,
则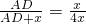 ,
,
AD= x.
x.
AF= x
x
∵△AFG∽△ABC,
∴ ,
,
∴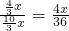 ,
,
解得:x= .
.
故选A.
点评:本题考查了展开图折叠成几何体的运用,相似三角形的判定与性质的运用.解答中应用隐含条件正方形的对边平行证明三角形相似从而求出线段的长度.
分析:如图,设正方体的棱长为x,则DE=x,FG=4x,根据相似三角形的性质可以用x表示出AD,再根据△AFG∽△ABC就可以求出正方体的棱长.
解答:
 解:由题意可知△ADE∽△AFG,
解:由题意可知△ADE∽△AFG,则
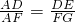 .
.设正方体的棱长为x,则DE=x,FG=4x,
则
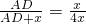 ,
,AD=
 x.
x.AF=
 x
x∵△AFG∽△ABC,
∴
 ,
,∴
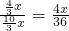 ,
,解得:x=
 .
.故选A.
点评:本题考查了展开图折叠成几何体的运用,相似三角形的判定与性质的运用.解答中应用隐含条件正方形的对边平行证明三角形相似从而求出线段的长度.

练习册系列答案
相关题目
 (2013•襄阳)在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是
(2013•襄阳)在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( )
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为( ) 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为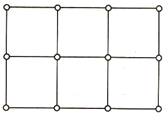 如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为________.
如图,在2×3矩形方格纸上,各个小正方形的顶点称为格点,则以格点为顶点的等腰直角三角形的个数为________.