Question

13．如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，AB为⊙O的直径．动点P从点A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以3cm/s的速度运动，P、Q两点同时出发，当其中一点到达端点时，另一点也随之停止运动．设运动时间为t，求：
（1）t分别为何值时，P、Q两点之间的距离是10cm？（四边形PQCD为平行四边形、等腰梯形？）
（2）t分别为何值时，直线PQ与⊙O相切、相离、相交？

Answer 1

分析 （1）根据速度乘时间，可得AP，BQ，根据线段的和差，可得OE的长，根据勾股定理，可得答案；
（2）根据PQ从相交到相切，由相切到相离，由相离到相切，再到相交，根据相切，可得PQ=AP+BQ，根据勾股定理，可得t值；根据小于第一次相切时相交，大于第一次相切的时间，小于第二次相切的时间时相离，根据大于第二次相切时再次相交，可得答案．

解答 解：（1）AP=t，BQ=26-3t，如图1：作PE⊥BC于E，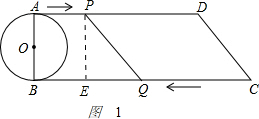

QE=26-4t．
由勾股定理，得
（26-4t）²+64=100，
解得t=5或8；
（2）当PQ与⊙O相切时，如图2，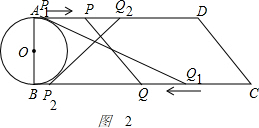
，
由相切，得PQ=AP+BQ=26-2t，
BE=26-4t，PE=8，
（26-4t）²+64=（26-2t）²
直线PQ与⊙O相切，t=8或$\frac{2}{3}$；
当26÷3=$\frac{26}{3}$，当t=$\frac{26}{3}$时运动停止，
相交0≤t＜$\frac{2}{3}$或8＜t≤$\frac{26}{3}$；
相离$\frac{2}{3}$＜t＜8．

点评 本题考查了圆的综合题，利用了勾股定理，理解直线由相交到相切，再到相切，最后相交是解题关键．