题目内容
 如图,AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,那么∠CAE=
如图,AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,那么∠CAE=考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:求出BD=CE和∠B的度数,根据SAS推出△ADB≌△AEC,推出∠C=∠B=40°,根据三角形内角和定理求出即可.
解答:解:∵BE=CD,
∴BE-DE=CD-DE,
∴BD=CE,
∵∠2=100°,∠BAE=60°,
∴∠B=∠2-∠BAE=40°,
∵在△ADB和△AEC中
∴△ADB≌△AEC,
∴∠C=∠B=40°,
∵∠2+∠C+∠CAE=180°,
∴∠CAE=180°-100°-40°=40°,
故答案为:40°.
∴BE-DE=CD-DE,
∴BD=CE,
∵∠2=100°,∠BAE=60°,
∴∠B=∠2-∠BAE=40°,
∵在△ADB和△AEC中
|
∴△ADB≌△AEC,
∴∠C=∠B=40°,
∵∠2+∠C+∠CAE=180°,
∴∠CAE=180°-100°-40°=40°,
故答案为:40°.
点评:本题考查了全等三角形的性质和判定,三角形的外角性质,三角形内角和定理的应用,解此题的关键是求出△ADB≌△AEC,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 如图,抛物线y=x2-2x-3与直线y=-x+b交于A,C两点,与x轴交于点A,B.点P为直线AC下方抛物线上的一个动点(不包括点A和点C),过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP.设点P的横坐标为m.
如图,抛物线y=x2-2x-3与直线y=-x+b交于A,C两点,与x轴交于点A,B.点P为直线AC下方抛物线上的一个动点(不包括点A和点C),过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP.设点P的横坐标为m.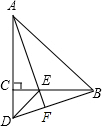 如图△ABC和△ECD都是等腰直角三角形,点C在AD上,AE的延长线交BD于点F,求证:AF⊥BD.
如图△ABC和△ECD都是等腰直角三角形,点C在AD上,AE的延长线交BD于点F,求证:AF⊥BD. 如图,点C、E、B、F在同一直线上,AC∥DF,∠A=∠D,CE=BF.求证:AB=DE.
如图,点C、E、B、F在同一直线上,AC∥DF,∠A=∠D,CE=BF.求证:AB=DE. 已知:如图,AB=DC,AE=BF,CE=DF,求证:AE∥BF.
已知:如图,AB=DC,AE=BF,CE=DF,求证:AE∥BF. 已知二次函数y=x2+2x+m的部分图象如下图所示,则关于x的一元二次方程x2+2x+m=0的解为
已知二次函数y=x2+2x+m的部分图象如下图所示,则关于x的一元二次方程x2+2x+m=0的解为 以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图(2)的有
以如图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换能得到图(2)的有