题目内容
12．如果-3ax+2yb9与2a3b2x+y是同类项，则x+y=4．分析 根据同类项的概念求解．
解答 解：∵-3ax+2yb9与2a3b2x+y是同类项，
∴$\left\{\begin{array}{l}{x+2y=3}\\{9=2x+y}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$，
则x+y=5-1=4．
故答案为：4．
点评 本题考查了同类项的知识，解答本题的关键是掌握同类项定义中的两个“相同”：相同字母的指数相同．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．
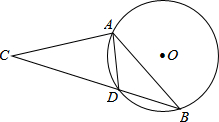如图，在⊙O中，弦AD等于半径，B为优弧AD上的一动点，等腰△ABC的底边BC所在直线经过点D．若⊙O的半径等于1，则OC的长不可能为（ ）
如图，在⊙O中，弦AD等于半径，B为优弧AD上的一动点，等腰△ABC的底边BC所在直线经过点D．若⊙O的半径等于1，则OC的长不可能为（ ）| A． | 2-$\sqrt{3}$ | B． | $\sqrt{3}$-1 | C． | 2 | D． | $\sqrt{3}$+1 |
7．下列各式中计算正确的是（ ）
| A． | $\sqrt{（-5）^{2}}$=-5 | B． | $\sqrt{9}$=±3 | C． | $\root{3}{（-2）^{3}}$=-2 | D． | （2$\sqrt{3}$）2=6 |
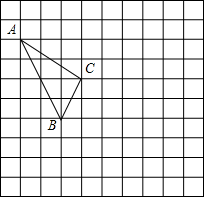已知△ABC的顶点A（-4，5），B（-2，1），完成下列问题：