题目内容
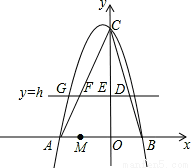
如图，已知抛物线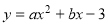
的对称轴为直线
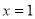，交
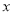轴于A、B两点，交
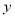轴于C点，其中B点的坐标为（3,0）。
（1）直接写出A点的坐标；
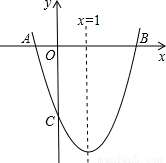
（2）求二次函数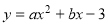的解析式。
（1）A点的坐标为（-1，0）;（2）y=x2-2x-3．
【解析】
试题分析：（1）由抛物线y=ax2+bx-3的对称轴为直线x=1，交x轴于A、B两点，其中B点的坐标为（3，0），根据二次函数的对称性，即可求得A点的坐标；
（2）利用待定系数法，将A（-1，0）、B（3，0）两点的坐标代入y=ax2+bx-3，即可求得二次函数y=ax2+bx-3的解析式．
试题解析：（1）A点的坐标为（-1，0）
（2）把A（-1，0）、B（3，0）两点的坐标代入y=ax2+bx-3，
得
，
解得
，
∴二次函数y=ax2+bx-3的解析式为y=x2-2x-3．
考点：二次函数综合题．
练习册系列答案
相关题目
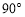的∠MON，我们给出如下定义：若点P在∠MON的内部或边界上，作PE⊥OM于点E，PF⊥ON于点F，则称PE+PF为点P相对于∠MON的“点角距离”，记为
．
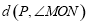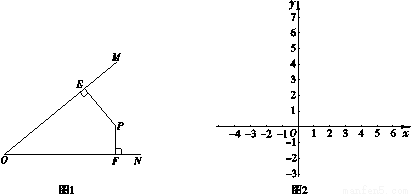
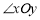，点P为第一象限内或两条坐标轴正半轴上的动点，且满足
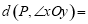5，点P运动形成的图形记为图形G．
，
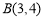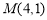，求
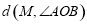的值；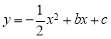
经过（2）中的A，B两点，点Q在A，B两点之间的抛物线上（点Q可与A，B两点重合），求当
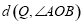取最大值时，点Q 的坐标．
，且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点，则满足上述条件且对称轴平行于y轴的抛物线条数是（ ）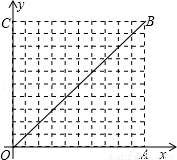
的最大值是（ ）
B．
C．1 D．2
B．
C．
D．
