题目内容
16.探究:如图①,在正方形ABCD中,点E在边BC上(点E不与点B、C重合),连结AE,过点E作AE⊥EF,EF交边CD于点F,求证:△ABE≌△ECF.拓展:如图②,△ABC是等边三角形,点D在边BC上(点D不与点B、C重合),连结AD,以AD为边作∠ADE=∠ABC,DE交边AC于点E,若AB=3,BD=x,CE=y,求y与x的函数关系式(不要求写出自变量x的取值范围).
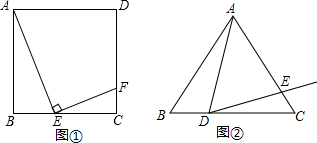
分析 (1)由正方形的性质和已知条件证明∠BAE=∠FEC,即可证明:△ABE∽△ECF;
(2)根据等边三角形的性质得到∠B=∠C=60°,于是得到∠BAD+∠ADB=120°,根据已知条件得到∠ADB+∠CDE=120°,等量代换得到∠BAD=∠CDE,推出△ABD∽△DCE,由相似三角形的性质得到$\frac{AB}{CD}=\frac{BD}{CE}$,代入数据即可得到结论.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)解:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAD+∠ADB=120°,
∵∠ADE=∠ABC,
∴∠ADE=60°,
∴∠ADB+∠CDE=120°,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴$\frac{AB}{CD}=\frac{BD}{CE}$,
∵AB=3,BD=x,CE=y,
∴$\frac{3}{3-x}=\frac{x}{y}$,
∴y=-$\frac{1}{3}$x2+x.
点评 本题考查了相似三角形的判定和性质,正方形的性质,等边三角形的性质,求二次函数的解析式,证得△ABD∽△DCE是解题的关键.

练习册系列答案
相关题目
11.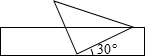 如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
 如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )
如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )| A. | 2cm | B. | 4cm | C. | 2$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
1.关于x的一元一次方程(a-1)x2+x+a2-1=0的一个解是0,则a的值为( )
| A. | 1 | B. | -l | C. | 1 或-1 | D. | 2 |
6. a、b两数在数轴上的位置如图所示,则下列各式正确的是( )
a、b两数在数轴上的位置如图所示,则下列各式正确的是( )
 a、b两数在数轴上的位置如图所示,则下列各式正确的是( )
a、b两数在数轴上的位置如图所示,则下列各式正确的是( )| A. | ab>0 | B. | a>-b | C. | a2-b2>0 | D. | |b-1|=1-b |
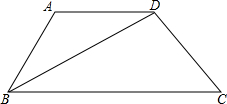 如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD.
如图,AD∥BC,BD平分∠ABC,则图中的等腰三角形是△ABD. 如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.
如图所示,网格中有△ABC和点D,请你找出另外两点E、F,在图中画出△DEF,使△ABC≌△DEF,且顶点A、B、C分别与D、E、F对应.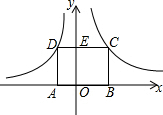 如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.
如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.