题目内容
5.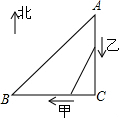 如图,A地在C地的正北方向,B地在C地的正西方向,AC=BC=6km,甲、乙两人分别从C、A两地同时骑摩托车出发,甲去往B地,速度为1km/min,乙去往C地,速度为2km/min,几分钟后,两人相距2$\sqrt{2}$km?
如图,A地在C地的正北方向,B地在C地的正西方向,AC=BC=6km,甲、乙两人分别从C、A两地同时骑摩托车出发,甲去往B地,速度为1km/min,乙去往C地,速度为2km/min,几分钟后,两人相距2$\sqrt{2}$km?
分析 设时间为x分钟,依题意得CF=x,则CE=6-2x,利用勾股定理列方程求解.
解答 解:如图,
∵AC=BC=6km,
设x分钟后,两人相距2$\sqrt{2}$km,依题意得CF=x,则CE=6-2x,
∴x2+(6-2x)2=(2$\sqrt{2}$)2.
解得x1=$\frac{1}{2}$,x2=$\frac{14}{5}$,
答:则$\frac{1}{2}$或$\frac{14}{5}$分钟后,两人相距2$\sqrt{2}$千米.
点评 此题考查一元二次方程的实际运用,勾股定理的运用,利用勾股定理建立方程是解决问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
17.下列合并同类项,结果正确的是( )
| A. | x4+x4=x8 | B. | 5m-2m+4m=7m | ||
| C. | 15a+4a-11=18a | D. | -9xy-2xy+11xy=xy |
 用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?
用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗? 如图,已知∠1=∠2,DE=CE,∠AEB=90°,求证:∠3=∠4.
如图,已知∠1=∠2,DE=CE,∠AEB=90°,求证:∠3=∠4.