题目内容
1.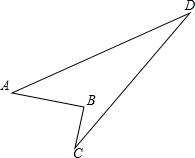 有一块土地,如图所示,已知AB=8,∠B=90°,BC=6,CD=24,AD=26,求这块土地的面积.
有一块土地,如图所示,已知AB=8,∠B=90°,BC=6,CD=24,AD=26,求这块土地的面积.
分析 连接AC,先根据勾股定理求出AC的长,再由勾股定理的逆定理判断出△ACD的形状,根据S四边形ABC=S△ACD-S△ABC即可得出结论.
解答 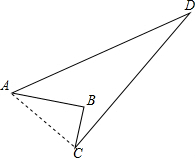 解:连接AC,
解:连接AC,
∵AB=8,∠B=90°,BC=6,
∴AC=$\sqrt{{8}^{2}+{6}^{2}}$=10.
∵CD=24,AD=26,
∴CD2=242=576,AD2=262=676,AC2=1002=100,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S四边形ABC=S△ACD-S△ABC
=$\frac{1}{2}$AC•CD-$\frac{1}{2}$AB•BC
=$\frac{1}{2}$×10×24-$\frac{1}{2}$×8×6
=120-24
=96.
答:这块土地的面积是96.
点评 本题考查的是勾股定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
9.如图,某建筑物由相同的若干个房间组成,该楼的三视图如图所示,试问:该楼有( )


| A. | 一层 | B. | 二层 | C. | 三层 | D. | 四层 |
16.如果60m表示“向北走60m”,那么“向南走20m”可以表示为( )
| A. | -20m | B. | -40m | C. | 20m | D. | 40m |
13.等腰三角形的一个角是90°,则它的底角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$cm,∠C=30°,点D从点C出发沿CA方向以每秒2cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,BC=5$\sqrt{3}$cm,∠C=30°,点D从点C出发沿CA方向以每秒2cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.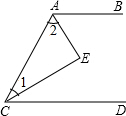 如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.
如图,AE平分∠BAC,CE平分∠ACD,且∠1+∠2=90°.试说明CD∥AB.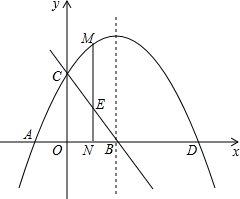 如图,抛物线y=ax2+bx+4与x轴交于A(-2,0),D两点,与y轴交于点C,对称轴x=3交x轴交于点B.
如图,抛物线y=ax2+bx+4与x轴交于A(-2,0),D两点,与y轴交于点C,对称轴x=3交x轴交于点B.