题目内容
1.如图,已知抛物线y=-$\frac{1}{2}$x2-2x+6与y轴交于点A,与x轴交于B、C两点,连接AC.(1)求直线AC的解析式;
(2)点P为直线AC上方抛物线上的一点,过点P作PD⊥AC点D,当线段PD的最长时,求点P的坐标;
(3)在(2)的条件下,连接PB,Q为抛物线上一动点,过点Q做QF⊥PB交直线PB于点F.若Q点的横坐标为t,抛物线的对称轴与AC交于点E,求t为何值时,EF=QE?

分析 (1)根据坐标轴上点的特点,令x=0,y=0,再用待定系数法求解即可;
(2)先判断出△PDE∽△AOC,得到PD=DE=$\frac{\sqrt{2}}{2}$PE,再建立PE=-$\frac{1}{2}$x2-2x+6-(x+6)=-$\frac{1}{2}$x2-3x,根据二次函数极值的确定方法即可;
(3)先求出直线PB解析式为y=-$\frac{3}{2}$x+3,再确定出QQ1的解析式,求出它和抛物线的交点坐标的横坐标即可.
解答 解:(1)令x=0,y=6,
∴A(0,6),
令y=0,-$\frac{1}{2}$x2-2x+6=0,
∴x1=2,x2=-6,
∴B(2,0),C(-6,0),
设直线AC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=6}\\{-6k+6=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=1}\\{b=6}\end{array}\right.$,
∴直线AC解析式为y=x+6,
(2)如图,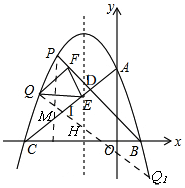 作PM∥y轴交AC于M,
作PM∥y轴交AC于M,
∴∠PMA=∠CAO,
∵∠PDM=∠AOC=90°,
∴△PDM∽△AOC
∵OA=OC,
∴PD=DM=$\frac{\sqrt{2}}{2}$PM,
设P(x,-$\frac{1}{2}$x2-2x+6),
∴M(x,x+6),
∴PM=-$\frac{1}{2}$x2-2x+6-(x+6)=-$\frac{1}{2}$x2-3x,
当x=-3时,PM最长,
把x=-3代入y=-$\frac{1}{2}$x2-2x+6=$\frac{15}{2}$,
∴P(-3,$\frac{15}{2}$);
(3)如图, 过Q作QQ1∥PB交抛物线对称轴于H,交AC于I,
过Q作QQ1∥PB交抛物线对称轴于H,交AC于I,
∵QF⊥PD,
∴QF⊥QQ1,
∵EF=QE,
∴∠EFQ=∠EQF,
∴∠EFD=∠EQH,
∴点E是ID的中点,
∵B(2,0),P(-3,$\frac{15}{2}$);
∴直线PB解析式为y=-$\frac{3}{2}$x+3,
∵直线AC解析式为y=x+6,
∴D(-$\frac{6}{5}$,$\frac{24}{5}$),
∵E(-2,4),
∴I(-$\frac{14}{5}$,$\frac{16}{5}$)
∵直线Q1Q∥PB,且过I
∴Q1Q解析式为y=-$\frac{3}{2}$x-1,
∵$\left\{\begin{array}{l}{y=-\frac{3}{2}x-1}\\{y=-\frac{1}{2}{x}^{2}-2x+6}\end{array}\right.$,
∴x=$\frac{-1±\sqrt{57}}{2}$,
∴t=$\frac{-1+\sqrt{57}}{2}$.
点评 此题是二次函数综合题,主要考查了坐标轴上点的特点,待定系数法,三角形的相似的性质和判定,对称的性质,解本题的关键是确定函数关系式.

 达州市图书馆今年4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图不完整的统计图表.
达州市图书馆今年4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图不完整的统计图表.八年级(1)班学生去新图书馆的次数统计表
| 去图书馆的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
| 人数 | 8 | 12 | a | 10 | 4 |
(1)填空:a=16,b=20;
(2)求扇形统计图中“0次”的扇形所占圆心角的度数;
(3)从全班去过该图书馆的同学中随机抽取1人,谈谈对新图书馆的印象和感受.求恰好抽中去过“4次及以上”的同学的概率.
| A. | 3,4,5 | B. | 6,8,10 | C. | 5,12,13 | D. | 2,3,4 |

 ;
;