题目内容
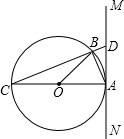
如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=
∠AOB.
(1)求证:MN是⊙O的切线;
(2)延长CB交MN于点D,求AD的长.
| 1 |
| 2 |
(1)求证:MN是⊙O的切线;
(2)延长CB交MN于点D,求AD的长.

(1)证明:∵AC是直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵∠BAM=
∠AOB=∠C,
∴∠BAM+∠BAC=90°,即∠CAM=90°.
∴MN是⊙O的切线.
(2)∵∠ABC=90°,AC=13,BC=12,
∴AB=5.
∵tanC=
=
,
∴
=
,
∴AD=
.
∴∠ABC=90°,∠C+∠BAC=90°.
∵∠BAM=
| 1 |
| 2 |
∴∠BAM+∠BAC=90°,即∠CAM=90°.
∴MN是⊙O的切线.
(2)∵∠ABC=90°,AC=13,BC=12,
∴AB=5.
∵tanC=
| AB |
| BC |
| AD |
| AC |
∴
| 5 |
| 12 |
| AD |
| 13 |
∴AD=
| 65 |
| 12 |

练习册系列答案
相关题目