Question

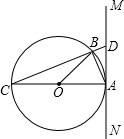
如图，已知A、B两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为（-1，0），半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是（　　）

A．2

B．1

C．2- 2 2

D．2- 2

Answer 1

若△ABE的面积最小，则AD与⊙C相切，连接CD，则CD⊥AD；
Rt△ACD中，CD=1，AC=OC+OA=3；
由勾股定理，得：AD=2

2

；
∴S_△ACD=

1

2

AD•CD=

2

；
易证得△AOE∽△ADC，
∴

S△AOE

S△ADC

=（

OA

AD

）²=（

2

2 2

）²=

1

2

，
即S_△AOE=

1

2

S_△ADC=

2

2

；
∴S_△ABE=S_△AOB-S_△AOE=

1

2

×2×2-

2

2

=2-

2

2

；
另利用相似三角形的对应边的比相等更简单！
故选C．