题目内容
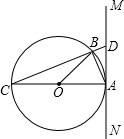
如图，AB是⊙O的直径，AC是弦，点D是
的中点，PD切⊙O于点D．
（1）求证：DP⊥AP；
（2）若PD=12，PC=8，求⊙O的半径R的长．
 |
| BC |
（1）求证：DP⊥AP；
（2）若PD=12，PC=8，求⊙O的半径R的长．
（1）证明：连接BC、OD，相交于点E；
∵点D是
的中点，
∴OD⊥BC，
∴∠CED=90°，
∵AB是⊙O的直径，
∵∠ACB=90°，
∵PD为⊙O的切线，
∴OD⊥PD，
∴∠PDE=90°
∴四边形PDEC为矩形，
∴DP⊥AP；
（2）由（1）可知四边形PDEC为矩形，
∴PD=CE=12，
∴BC=2CE=24；
∵PD2=PC•PA，
∴PA=
=
=18，
∴AC=PA-PC=18-8=10；
∵AB2=AC2+BC2=102+242=676，
∴AB=26，
∴⊙O的半径R=13．
∵点D是
|
| BC |
∴OD⊥BC，
∴∠CED=90°，
∵AB是⊙O的直径，
∵∠ACB=90°，
∵PD为⊙O的切线，
∴OD⊥PD，
∴∠PDE=90°
∴四边形PDEC为矩形，
∴DP⊥AP；
（2）由（1）可知四边形PDEC为矩形，
∴PD=CE=12，
∴BC=2CE=24；
∵PD2=PC•PA，
∴PA=
| PD2 |
| PC |
| 122 |
| 8 |
∴AC=PA-PC=18-8=10；
∵AB2=AC2+BC2=102+242=676，
∴AB=26，
∴⊙O的半径R=13．
练习册系列答案
相关题目
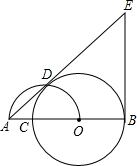
，作⊙O′的切线PE切⊙O′于点E．若PC=4，CD=8，⊙O的半径为5．
