Question

如图，已知点E,F分别是□ABCD的边BC,AD上的中点，且∠BAC=90°．

（1）求证：四边形AECF是菱形；

（2）若∠B=30°，BC=10，求菱形AECF面积．

Answer 1

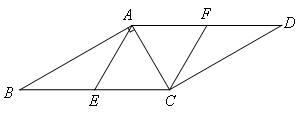
（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC.

在Rt△ABC中，∠BAC=90°，点E是BC边的中点，

∴AE=CE=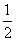BC.

同理，AF=CF=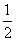AD.

∴AF=CE.…………………………………………………………………………………………1

∴四边形AECF是平行四边形.

∴平行四边形AECF是菱形.……………………………………………………………………2

（2）解：在Rt△ABC中，∠BAC=90°，∠B=30°，BC=10，

∴AC=5，AB=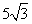.……………………………………………………………………………3

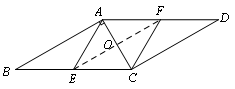
连接EF交于点O，

∴AC⊥EF于点O，点O是AC中点.

∴OE=.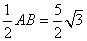

∴EF=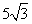.………………………………………………4

∴菱形AECF的面积是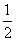AC·EF=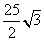．……………………………………………………5