题目内容
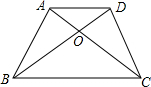 如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD交于点O,AD:BC=1:2.
如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD交于点O,AD:BC=1:2.(1)设
| BA |
| a |
| BC |
| b |
| a |
| b |
| BO |
(2)先化简,再求作:
| 3 |
| 2 |
| a |
| b |
| a |
| b |
考点:*平面向量
专题:
分析:(1)由AD∥BC,可得△AOD∽△COB,然后由相似三角形的对应边成比例,求得
=
=2,利用三角函数的知识即可求得
、
的长,继而求得
.
(2)利用平面向量的运算法则求解即可求得答案.
| BO |
| OD |
| BC |
| AD |
| AD |
| BD |
| BO |
(2)利用平面向量的运算法则求解即可求得答案.
解答:解:(1)∵AD∥BC,AD:BC=1:2,
∴△AOD∽△COB,
∴
=
=2,
=
=
,
∴
=
+
=
+
,
∴
=
=
+
;
(2)
(2
+
)-2(
+
)=3
+
-2
-2
=
-
.
如图:
即为所求.
=
-
=
+
-
=
-
.
∴△AOD∽△COB,
∴
| BO |
| OD |
| BC |
| AD |
| AD |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| b |
∴
| BD |
| BA |
| AD |
| a |
| 1 |
| 2 |
| b |
∴
| BO |
| 2 |
| 3 |
| BD |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |

(2)
| 3 |
| 2 |
| a |
| b |
| a |
| b |
| a |
| 3 |
| 2 |
| b |
| a |
| b |
| a |
| 1 |
| 2 |
| b |
如图:
| CD |
| CD |
| BD |
| BC |
| a |
| 1 |
| 2 |
| b |
| b |
| a |
| 1 |
| 2 |
| b |
点评:此题考查了平面向量的知识以及相似三角形的判定与性质.此题难度适中,注意掌握三角形法则的应用,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
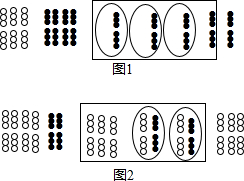 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )
我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)的过程.按照这种方法,图2表示的过程应是在计算( )| A、(-5)+(-2) |
| B、(-5)+2 |
| C、5+(-2) |
| D、5+2 |
| 1 |
| 6 |
| A、6 | ||
| B、-6 | ||
C、
| ||
D、-
|
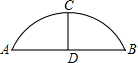 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24m,拱高为8m,则拱的半径为( )
如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24m,拱高为8m,则拱的半径为( )| A、12m | B、8m |
| C、14m | D、13m |
下列说法中正确的个数有( )
①经过一点有且只有一条直线;
②连接两点的线段叫做两点之间的距离;
③射线比直线短;
④ABC三点在同一直线上且AB=BC,则B是线段AC的中点;
⑤在同一平面内,两条直线的位置关系有两种:平行与相交;
⑥在8:30时,时钟上时针和分针的夹角是75°.
①经过一点有且只有一条直线;
②连接两点的线段叫做两点之间的距离;
③射线比直线短;
④ABC三点在同一直线上且AB=BC,则B是线段AC的中点;
⑤在同一平面内,两条直线的位置关系有两种:平行与相交;
⑥在8:30时,时钟上时针和分针的夹角是75°.
| A、1个 | B、2个 | C、3个 | D、4个 |
某校有21名学生参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
| A、最高分 | B、平均分 |
| C、极差 | D、中位数 |