题目内容
13.某市某楼盘准备以每平方米6000元的均价对外销售,由于购房者持币观望,销售不畅,为了加快资金周转,该房地产开发商对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.求平均每次下调的百分率.分析 设平均每次下调的百分率为x,利用预订每平方米销售价格×(1-每次下调的百分率)2=开盘每平方米销售价格列方程解答即可.
解答 解:设平均每次降价的百分率是x,根据题意列方程得,
6000(1-x)2=4860,
解得:x1=10%,x2=1.9(不合题意,舍去);
答:平均每次降价的百分率为10%.
点评 此题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
1.若( )•3ab2=6a2b3,则括号内应填的代数式是( )
| A. | 2a | B. | ab | C. | 2ab | D. | 3ab |
5.某公司销售一种进价为每个20元的计算器,其销售量y(万个)与销售价格x(元)的变化如表:
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的x与y之间对应关系,用所学过的一次函数或二次函数的有关知识写出y(万个)与x(元)的函数表达式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元)的函数表达式,并说明销售价格定为多少元时,净利润最大?最大值是多少?
| 价格x/元 | … | 30 | 40 | 50 | 60 | … |
| 销售量y/万个 | … | 5 | 4 | 3 | 2 | … |
(1)观察并分析表中的x与y之间对应关系,用所学过的一次函数或二次函数的有关知识写出y(万个)与x(元)的函数表达式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元)的函数表达式,并说明销售价格定为多少元时,净利润最大?最大值是多少?
2.某地电话拨号人网有A、B两种计费方式.用户可任选其一;A为计时制:3元/小时;B为包月制;48元/月(限一部个人住宅电话人网).此外,每-种计费方式都得加收通讯费1.2元/时.
(1)按两种计费方式.把每月上网5小时、10小时、15小时、20小时、25小时的费用求出来,填入下表.
(2)当用户上网多少小时两种计费方式所交费用相同?
(3)由此可推测什么情况下选择计时制较划算?什么情况下选择包月制较划算?
(1)按两种计费方式.把每月上网5小时、10小时、15小时、20小时、25小时的费用求出来,填入下表.
| 时间(小时) | 5 | 10 | 15 | 20 | 25 |
| 计时制的费用(元) | 21 | 42 | 63 | 84 | 105 |
| 包月制的费用(元) | 54 | 60 | 66 | 72 | 78 |
(3)由此可推测什么情况下选择计时制较划算?什么情况下选择包月制较划算?
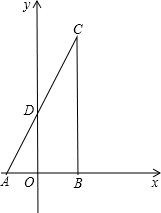 已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,
已知△ABC中,∠B=90°,∠A=60°,AB=6,把它放在平面坐标系中,使A,B两点关于y轴对称,边AC交y轴于点D,如图所示,点P是AC边上的动点,点E是x轴上的动点,且PB=PE,设PA=t,