题目内容
观察下列等式:
第1个等式:a1=
=
×(1-
);
第2个等式:a2=
=
×(
-
);
第3个等式:a3=
=
×(
-
);
第4个等式:a4=
=
×(
-
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=______;
(2)用含有n的代数式表示第n个等式:an=______=______(n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
第1个等式:a1=
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
第2个等式:a2=
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
第3个等式:a3=
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
第4个等式:a4=
| 1 |
| 7×9 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5=______;
(2)用含有n的代数式表示第n个等式:an=______=______(n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
根据观察知答案分别为:
(1)
;
×(
-
);
(2)
;
×(
-
);
(3)a1+a2+a3+a4+…+a100的
=
×(1-
)+
×(
-
)+
×(
-
)+
×(
-
)+…+
×(
-
)
=
(1-
+
-
+
-
+
-
+…+
-
)
=
(1-
)
=
×
=
.
(1)
| 1 |
| 9×11 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 11 |
(2)
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
(3)a1+a2+a3+a4+…+a100的
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2 |
| 1 |
| 199 |
| 1 |
| 201 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 199 |
| 1 |
| 201 |
=
| 1 |
| 2 |
| 1 |
| 201 |
=
| 1 |
| 2 |
| 200 |
| 201 |
=
| 100 |
| 201 |

练习册系列答案
相关题目
 ;
; ;
; ;
; ;
; = = ;
= = ; = = (n为正整数);
= = (n为正整数); 的值.
的值.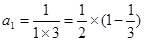 ;
; ;
;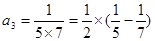 ;
; ;
;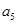 =
= ;
=
= ;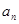 =
= (n为正整数);
=
= (n为正整数);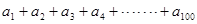 的值.
的值.