题目内容
18.若n为整数,且$\sqrt{{n}^{2}+9n+30}$是自然数,则n=-14或-7或-2或5.分析 设$\sqrt{{n}^{2}+9n+30}$=p,再把等式两边同时乘以4,利用平方差公式把等式左边化为两个因式积的形式,列出关于p、n的方程组,求出n的值即可.
解答 解:∵设$\sqrt{{n}^{2}+9n+30}$=p(P为非负整数),则n2+9n+30=p2,
∴4n2+36n+120=4p2,
∴(2n+9)2+39=4p2,
∴(2p+2n+9)(2p-2n-9)=39,
∴$\left\{\begin{array}{l}2p+2n+9=1\\ 2p-2n-9=39\end{array}\right.$或$\left\{\begin{array}{l}2p+2n+9=39\\ 2p-2n-9=1\end{array}\right.$或$\left\{\begin{array}{l}2p+2n+9=3\\ 2p-2n-9=13\end{array}\right.$或$\left\{\begin{array}{l}2p+2n+9=13\\ 2p-2n-9=3\end{array}\right.$,
解得$\left\{\begin{array}{l}p=10\\ n=-14\end{array}\right.$或$\left\{\begin{array}{l}p=10\\ n=5\end{array}\right.$或$\left\{\begin{array}{l}p=4\\ n=-7\end{array}\right.$或$\left\{\begin{array}{l}p=4\\ n=-2\end{array}\right.$,
∴n=-14或-7或-2或5.
故答案为:-14或-7或-2或5.
点评 本题考查的是二次根式的性质与化简,先根据题意把原式化为两个因式积的形式是解答此题的关键.

 如图魔方共由多少个小正方体组成( )
如图魔方共由多少个小正方体组成( )| A. | 18 | B. | 19 | C. | 26 | D. | 27 |
 如图,△PQR是△ABC经过某种变换后得到的图形,如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为( )
如图,△PQR是△ABC经过某种变换后得到的图形,如果△ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标为( )| A. | (-a,b) | B. | (a,-b) | C. | (-a,-b) | D. | (-b,-a) |
 如图是由火柴棍搭成的几何图案,则第n个图案中的火柴棍的根数为(用含n的式子表示)( )
如图是由火柴棍搭成的几何图案,则第n个图案中的火柴棍的根数为(用含n的式子表示)( )| A. | 4n | B. | 2n(n-1) | C. | 2n(n+1) | D. | 4n(n+2) |
| A. | 510×52=520 | B. | (-2ab3)3=8a3b9 | ||
| C. | x(2x+5)=2x2+5 | D. | (8x2y3-4x2y)÷2xy=4xy2-2x |
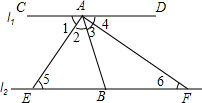 如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.
如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF. 图中是德国现代建筑师丹尼尔•里伯斯金设计的“时间迷宫”挂钟,它直观地表达出了设计师对时间的理解:时间是迷宫一般的存在--“若干抽象的连接和颇具玩味的互动”.在挂钟所在平面内,通过测量、画图等操作方式判断:AB,CD所在直线的位置关系是相交(填“相交”或“平行”),图中∠1与∠2的大小关系是∠1>∠2.(填“>”或“=”或“<”)
图中是德国现代建筑师丹尼尔•里伯斯金设计的“时间迷宫”挂钟,它直观地表达出了设计师对时间的理解:时间是迷宫一般的存在--“若干抽象的连接和颇具玩味的互动”.在挂钟所在平面内,通过测量、画图等操作方式判断:AB,CD所在直线的位置关系是相交(填“相交”或“平行”),图中∠1与∠2的大小关系是∠1>∠2.(填“>”或“=”或“<”)