题目内容
15. 如图,△AEC是等腰直角三角形,B为斜边AE上一点,△ABc经过旋转后到达△CDE的位置.则∠CED=45度,∠AED=90度.
如图,△AEC是等腰直角三角形,B为斜边AE上一点,△ABc经过旋转后到达△CDE的位置.则∠CED=45度,∠AED=90度.
分析 由等腰直角三角形的性质得出∠A=∠ABC=45°,由旋转的性质得出△CDE≌△CBA,由全等三角形的性质得出∠CED=∠A=45°,∠AED=∠ABC+∠CED,即可得出结果.
解答 解:∵△AEC是等腰直角三角形,
∴∠A=∠ABC=45°,
由旋转的性质得:△CDE≌△CBA,
∴∠CED=∠A=45°,∠AED=∠ABC+∠CED=90°;
故答案为:45,90.
点评 本题考查了旋转的性质、等腰直角三角形的性质、全等三角形的性质;熟练掌握旋转的性质,求出∠CED=∠A=45°是解决问题的关键.

练习册系列答案
相关题目
3.下列等式正确的是( )
| A. | 1+(-3)=$\frac{1}{3}$ | B. | -(-1)=-1 | C. | |-2|=2 | D. | (-2)×3=6 |
20.今年昭通市4月5日,这一天最低气温8℃,最高气温26℃,则昭通市这一天气温t(℃)的变化范围是( )
| A. | t>8 | B. | t≤26 | C. | 8<t<26 | D. | 8≤t≤26 |
7.三角形的高、中线、角平分线都是( )
| A. | 直线 | B. | 射线 | ||
| C. | 线段 | D. | 以上三种情况都有 |
5.下面那个图形不能折成一个正方体( )
| A. |  | B. |  | C. |  | D. |  |
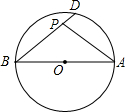 如图,AB是⊙O的直径,点D在⊙O上,∠ABD=40°,动点P在弦BD上,则∠PAB可能为此题答案不唯一,如40°度.(写出一个符合条件的度数即可)
如图,AB是⊙O的直径,点D在⊙O上,∠ABD=40°,动点P在弦BD上,则∠PAB可能为此题答案不唯一,如40°度.(写出一个符合条件的度数即可)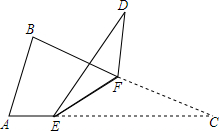 如图,将△ABC沿着EF翻折,若∠AED=130°,∠BFD=70°,则∠D=30°.
如图,将△ABC沿着EF翻折,若∠AED=130°,∠BFD=70°,则∠D=30°. 如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形中小箭头的方向是向上(填写:上、下、左、右).
如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形中小箭头的方向是向上(填写:上、下、左、右).