题目内容
10.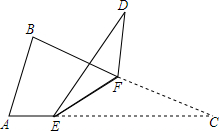 如图,将△ABC沿着EF翻折,若∠AED=130°,∠BFD=70°,则∠D=30°.
如图,将△ABC沿着EF翻折,若∠AED=130°,∠BFD=70°,则∠D=30°.
分析 连接CD,由翻折变换的性质得出CE=DE,CF=DF,由等腰三角形的性质得出∠ECD=∠EDC,∠FCD=∠FDC,由三角形的外角性质得出∠EDC=$\frac{1}{2}$∠AED=65°,∠FDC=$\frac{1}{2}$∠BFD=35°,即可得出结果.
解答 解:连接CD,如图所示:
由翻折变换的性质得:CE=DE,CF=DF,
∴∠ECD=∠EDC,∠FCD=∠FDC,
∵∠AED=130°=∠ECD+∠EDC,∠BFD=70°=∠FCD=∠FDC,
∴∠EDC=$\frac{1}{2}$∠AED=65°,∠FDC=$\frac{1}{2}$∠BFD=35°,
∴∠EDF=65°-35°=30°.
故答案为:30°.
点评 本题考查了翻折变换的性质、等腰三角形的性质、三角形的外角性质;熟练掌握翻折变换的性质,由等腰三角形和三角形的外角性质求出∠EDC和∠FDC是解题的关键.

练习册系列答案
相关题目
1.已知用4个矿泉水空瓶可换1瓶矿泉水,现有15个矿泉水空瓶若不再添钱,最多可喝矿泉水( )瓶.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.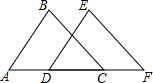 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )| A. | BC=EF | B. | ∠A=∠EDF | C. | AB∥DE | D. | ∠BCA=∠F |
2.如果点(a,1-a)在第四象限,那么a的取值范围是( )
| A. | 0<a<1 | B. | -1<a<0 | C. | a<0 | D. | a>1 |
19. 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )
 如图1,线段a、b,图2中线段AB表示的是( )
如图1,线段a、b,图2中线段AB表示的是( )| A. | a-b | B. | a+b | C. | a-2b | D. | 2a-b |
20.若|x+1|+(y-2)2=0,则xy的值是( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
 如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P. 如图,△AEC是等腰直角三角形,B为斜边AE上一点,△ABc经过旋转后到达△CDE的位置.则∠CED=45度,∠AED=90度.
如图,△AEC是等腰直角三角形,B为斜边AE上一点,△ABc经过旋转后到达△CDE的位置.则∠CED=45度,∠AED=90度.