题目内容
7.方程组$\left\{\begin{array}{l}{x+y=1}\\{y+z=2}\\{z+x=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$.分析 先用含z的代数式表示x、y,即解关于x,y的方程组,再代入x+y=1中可得.
解答 解:$\left\{\begin{array}{l}{x+y=1(1)}\\{y+z=2(2)}\\{z+x=3(3)}\end{array}\right.$.
由(2)、(3)分别得到:
y=2-z,x=3-z,
将其代入(1),得
2-z+3-z=1,
解得z=2,
所以y=2-2=0,x=3-2=1.
所以原方程组的解集为:$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$.
故答案是:$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=2}\end{array}\right.$.
点评 本题考查了解三元一次方程组的解法,有加减法和代入法两种,一般选用加减法解二元一次方程组较简单.

练习册系列答案
相关题目
18.式子$\frac{2x+1}{\sqrt{x-1}}$有意义的x的取值范围是( )
| A. | x<1 | B. | x≠1 | C. | x≥1 | D. | x>1 |
15.如图,小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则分别表示父亲、母亲离家距离与时间之间关系的是( )
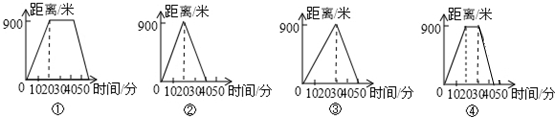

| A. | ①③ | B. | ①② | C. | ④② | D. | ④③ |
2.某校初一年级到礼堂开会,若每条长凳坐5人,则少10条长凳;若每条长凳坐6人,则又多余2条长凳.如果设学生数为x人,长凳为y条,根据题意可列方程组( )
| A. | $\left\{\begin{array}{l}{x=5y+5×10}\\{x=6y-6×2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5y-5×10}\\{x=6y+6×2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=5y-10}\\{x=6y+2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5y+10}\\{x=6y-2}\end{array}\right.$ |
12.$\sqrt{(-5)^{2}}$化简后的结果是( )
| A. | $\sqrt{5}$ | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
19.某市2013年投入教育经费2亿元,为了发展教育事业,该市每年教育经费的年增长率均为x,从2013年到2015年共投入教育经费9.5亿元,则下列方程正确的是( )
| A. | 2x2=9.5 | B. | 2(1+x)=9.5 | ||
| C. | 2(1+x)2=9.5 | D. | 2+2(1+x)+2(1+x)2=9.5 |
17.若不等式组$\left\{\begin{array}{l}{1<x≤2}\\{x>m}\end{array}\right.$有解,则m的取值范围是( )
| A. | m≥2 | B. | m<1 | C. | m>2 | D. | m<2 |