题目内容
14.在Rt△ABC中,∠C=90°,a=2,b=1,则tanA=2,cosA=$\frac{\sqrt{5}}{5}$,sinB=$\frac{\sqrt{5}}{5}$.分析 首先利用勾股定理求得斜边c的长,然后利用三角函数的定义求解.
解答 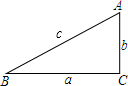 解:如图,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
解:如图,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
则tanA=$\frac{a}{b}$=2,cosA=$\frac{b}{c}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,sinB=$\frac{b}{c}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
故答案是:2,$\frac{\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
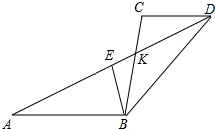 如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.
如图,已知线段AB∥CD,AD与BC相交于点K,∠ABC的角平线分BE交AD于E,当AE=$\frac{1}{2}$AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.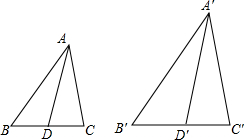 如图,D、D′分别是△ABC和△A′B′C′的边BC、B′C′的中点,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{AD}{A′D′}$,求证:△ABC∽△A′B′C′.
如图,D、D′分别是△ABC和△A′B′C′的边BC、B′C′的中点,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{AD}{A′D′}$,求证:△ABC∽△A′B′C′.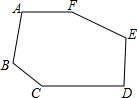 如图,六边形ABCDEF,AB∥DE,且∠A=110°,∠B=120°,∠E=100°,∠D=90°,求六边形ABCDEF其它内角的度数.
如图,六边形ABCDEF,AB∥DE,且∠A=110°,∠B=120°,∠E=100°,∠D=90°,求六边形ABCDEF其它内角的度数.