题目内容
6.已知△ABC为正三角形,点M的射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,直线BN与AM相交于Q点,如图①②③.(1)∠BQM等于多少度?并利用图③证明你的结论;
(2)如图②.若BP垂直AM于点P,求证:BQ=2PQ.
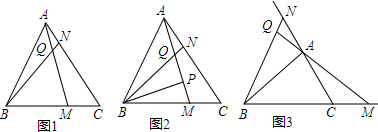
分析 (1)在图3中,根据三角形外角的性质及等边三角形的性质得出∠BAN=∠ACM=120°,由全等三角形的判定定理得出△ABN≌△CAM,再由三角形外角的性质即可得出结论;
(2)根据垂直的定义得到∠BPQ=90°,根据三角形的内角和得到∠PBQ=30°,由直角三角形的性质得到结论.
解答 解:(1)∠BQM=60°,
理由:如图3,∵△ABC是等边三角形,
∴∠BAN=∠ACM=60°,
∵BM=CN,AC=BC,
∴AN=CM,
在△ABN和△CAM中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAN=∠ACM}\\{AN=CM}\end{array}\right.$,
∴△ABN≌△CAM,
∴∠N=∠M,
∴∠BQM=∠N+∠QAN=∠M+∠CAM=∠ACB=60°;
(2)∵∠BQM=60°,
∵BP⊥AM,
∴∠BPQ=90°,
∴∠PBQ=30°,
∴BQ=2PQ.
点评 本题考查的是等边三角形的性质,全等三角形的判定与性质及三角形外角的性质,根据题意判断出△ABN≌△CAM是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列是二次函数的是( )
| A. | y=ax2+bx+c | B. | y=$\frac{1}{{x}^{2}}$+x | C. | y=x2-(x+7)2 | D. | y=(x+1)(2x-1) |
5.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{21}$ |

 如图,已知抛物线的顶点为M(2,-4),且过点A(-1,5),连结AM交x轴于点B.
如图,已知抛物线的顶点为M(2,-4),且过点A(-1,5),连结AM交x轴于点B.