题目内容
在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
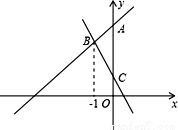
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范围.
(1)①B(-1,3);k=1;②、1.5;(2)2<k<4. 【解析】试题分析:(1)将点B的横坐标代入y=-2x+1得出点B的纵坐标,将点B的坐标代入y=kx+4求出k的值;根据解析式求出A、C的坐标,然后进行计算;(2)用k的代数式表示点E的横坐标,然后根据不等式求出k的取值. 试题解析:(1)①将x=-1代入y=-2x+1得:y=-2×(-1)+1=3,∴点B的坐标为(-1,3...
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
表格描述的是y与x之间的函数关系:
x | … | -2 | 0 | 2 | 4 | … |
y=kx+b | … | 3 | -1 | m | n | … |
则m与n的大小关系是____________.
m>n 【解析】∵当x=?2,y=3,x=0,y=?1, ∴y随着x的增大而减小, ∵2<4, ∴m>n. 故答案为:m>n.

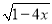 +
+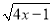 +
+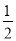 .求
.求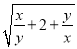 -
-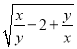 的值.
的值.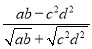 =______.
=______.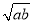 、
、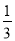
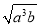 、
、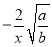 是同类二次根式.…(____)
是同类二次根式.…(____) +(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( )
+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( )