题目内容
18.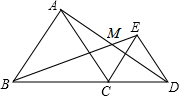 如图所示,△ABC与△CDE都是等边三角形,AD与BE交于点M.
如图所示,△ABC与△CDE都是等边三角形,AD与BE交于点M.(1)求证:AD=BE;
(2)联结MC,求证:∠BMC=∠DMC.
分析 (1)根据等边三角形性质得出AC=BC,CE=CD,∠ACB=∠ECD=60°,求出∠BCE=∠ACD,根据SAS推出两三角形全等即可;
(2)作CH⊥BE于H,CQ⊥AD于Q,如图,根据全等三角形的性质得到S△ACD=S△BCE,由于$\frac{1}{2}$AD•CH=$\frac{1}{2}$BE•CQ,于是得CQ=CH,然后根据角平分线的判定定理即可得到结论.
解答 (1)证明:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
即∠BCE=∠ACD,
∵在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,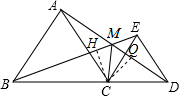
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)作CH⊥BE于H,CQ⊥AD于Q,如图,
∵△ACD≌△BCE,
∴S△ACD=S△BCE,
∴$\frac{1}{2}$AD•CH=$\frac{1}{2}$BE•CQ,
∴CQ=CH,
∴CO平分∠BOD.
点评 本题考查了三角形全等的判定和性质及等边三角形的性质;普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS.同时还要结合等边三角形的性质,创造条件证明三角形全等是正确解答本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8.函数y=kx的图象经过点P(3,-2),则k的值是( )
| A. | 1 | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -6 |
9.点P(2,-3)关于原点对称的点的坐标是( )
| A. | (-2,-3) | B. | (2,3) | C. | (-2,3) | D. | (-3,2) |
 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(-1,0)点(如图所示),康康依据图象写出了四个结论:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且经过(-1,0)点(如图所示),康康依据图象写出了四个结论: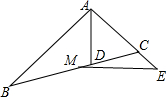 如图所示,在△ABC中,AD是∠BAC的平分线,M是BC的中点,ME⊥AD且交AC的延长线于E,CE=$\frac{1}{2}$CD,求证:∠ACB=2∠B.
如图所示,在△ABC中,AD是∠BAC的平分线,M是BC的中点,ME⊥AD且交AC的延长线于E,CE=$\frac{1}{2}$CD,求证:∠ACB=2∠B.