题目内容
 如图,要设计一个等腰梯形的花坛,花坛上底长72m,下底长112m,上下底相距60m,在两腰中点连线处有一条横向通道,上下底之间有两条纵向通道(如图阴影部分),各通道的宽度相等,通道的所有面积是梯形面积的
如图,要设计一个等腰梯形的花坛,花坛上底长72m,下底长112m,上下底相距60m,在两腰中点连线处有一条横向通道,上下底之间有两条纵向通道(如图阴影部分),各通道的宽度相等,通道的所有面积是梯形面积的| 7 |
| 184 |
考点:一元二次方程的应用,等腰梯形的性质
专题:几何图形问题
分析:找出题中的等量关系即通道面积是梯形面积的
,根据梯形的面积公式即可求解.
| 7 |
| 184 |
解答:解:设通道的宽为x米,依题意得:
2×60x+
(72+112)x-2x2=
×
×60×(72+112)
化简得:x2-106x+105=0,
(x-1)(x-105)=0
x1=1,x2=105(不合题意,舍去)
故取x=1
答:通道的宽为1米.
2×60x+
| 1 |
| 2 |
| 7 |
| 184 |
| 1 |
| 2 |
化简得:x2-106x+105=0,
(x-1)(x-105)=0
x1=1,x2=105(不合题意,舍去)
故取x=1
答:通道的宽为1米.
点评:本题主要考查一元二次方程的应用,解题的关键是得到通道的总面积,注意两个梯形的中位线是同一条.

练习册系列答案
相关题目
下列调查中,适合抽样调查的是( )
| A、调查某种胶囊中铬的含量 |
| B、了解某班学生对影片《暮光之城》的关注度 |
| C、对我国首艘航空母舰“辽宁号”零件的检查 |
| D、调查重庆市民对“钓鱼岛”事件的态度 |

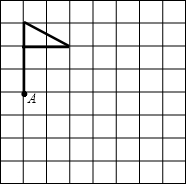 如图,方格中是美丽可爱的小彩旗图形,请将小彩旗向右平移四个单位(每小方格边长为1个单位),其中A点平移到A1位置,再将平移后以点A1为旋转中心顺时针方向旋转90°(只要求画出平移后的图形,不要求写出作图步骤和过程)
如图,方格中是美丽可爱的小彩旗图形,请将小彩旗向右平移四个单位(每小方格边长为1个单位),其中A点平移到A1位置,再将平移后以点A1为旋转中心顺时针方向旋转90°(只要求画出平移后的图形,不要求写出作图步骤和过程) 十一黄金周的夜晚,小明在某公园看到如图所示彩灯图案,该图案中心有一盏灯,有里向外,第二层有6盏灯,第三层有12盏灯,以此类推,则第8层有
十一黄金周的夜晚,小明在某公园看到如图所示彩灯图案,该图案中心有一盏灯,有里向外,第二层有6盏灯,第三层有12盏灯,以此类推,则第8层有 ①如图,线段AB与A1B1关于某点对称,请在图中画出这个点并写出这个点的坐标.
①如图,线段AB与A1B1关于某点对称,请在图中画出这个点并写出这个点的坐标.