题目内容
20.解关于x的不等式组:$\left\{\begin{array}{l}{9(a+1)x>9ax+8}\\{a(x-2)>x-3}\end{array}\right.$.分析 分别求出不等式组的解集,再分a>1与a<1两种情况进行讨论.
解答 解:$\left\{\begin{array}{l}{9(a+1)x>9ax+8①}\\{a(x-2)>x-3②}\end{array}\right.$,
由①得,x>$\frac{8}{9}$,
由②得,(a-1)x>2a-3,
当a>1时,则x>$\frac{2a-3}{a-1}$,当a<1时,则x<$\frac{2a-3}{a-1}$;
①当a>1且$\frac{2a-3}{a-1}$>$\frac{8}{9}$时,解得a>$\frac{19}{10}$,
所以,当a>$\frac{19}{10}$时,不等式组的解集为x>$\frac{2a-3}{a-1}$,
②当a>1且$\frac{2a-3}{a-1}$<$\frac{8}{9}$时,解得1<a<$\frac{19}{10}$,
所以,当1<a<$\frac{19}{10}$,不等式组的解集为x>$\frac{8}{9}$;
③当a<1且$\frac{2a-3}{a-1}$>$\frac{8}{9}$时,解得a<1,
所以当a<1,不等式组的解集为$\frac{8}{9}$<x<$\frac{2a-3}{a-1}$;
当a<1且$\frac{2a-3}{a-1}$<$\frac{8}{9}$时,不存在,
所以,不等式组无解.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.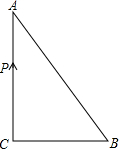 如图,在Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点P从点C出发,以2cm/s的速度沿CA、AB移动到B,则点P出发( )时,可使S△BCP=$\frac{1}{4}$S△ABC.
如图,在Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点P从点C出发,以2cm/s的速度沿CA、AB移动到B,则点P出发( )时,可使S△BCP=$\frac{1}{4}$S△ABC.
 如图,在Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点P从点C出发,以2cm/s的速度沿CA、AB移动到B,则点P出发( )时,可使S△BCP=$\frac{1}{4}$S△ABC.
如图,在Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点P从点C出发,以2cm/s的速度沿CA、AB移动到B,则点P出发( )时,可使S△BCP=$\frac{1}{4}$S△ABC.| A. | 1s | B. | $\frac{31}{4}$s | C. | 1s或$\frac{31}{4}$s | D. | 2s |
10.下列式子化简不正确的是( )
| A. | +(-5)=-5 | B. | -(-0.5)=0.5 | C. | -|+3|=-3 | D. | -(+1$\frac{1}{2}$)=1$\frac{1}{2}$ |
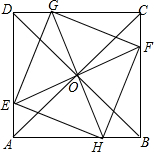 已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.
已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.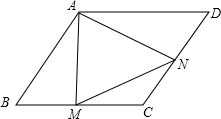 如图,已知菱形ABCD中,∠BAD=120°,M为BC上一点,N为CD上一点,求证:若△AMN有一个内角等于60°,则△AMN为等边三角形.
如图,已知菱形ABCD中,∠BAD=120°,M为BC上一点,N为CD上一点,求证:若△AMN有一个内角等于60°,则△AMN为等边三角形.