题目内容
15.已知函数y=(m-1)x${\;}^{{m}^{2}-1}$+1是一次函数,则m=$±\sqrt{2}$.分析 根据一次函数的定义列方程即可得到结论.
解答 解:一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
则得到m2-1=1,
∴m=±$\sqrt{2}$,
故答案为:$±\sqrt{2}$.
点评 本题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.k≠0是考查的重点.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
3.下列说法正确的是( )
| A. | 直线a、b都经过点m | B. | 直线AB、CD都经过点M | ||
| C. | 延长射线AB到C | D. | 线段、射线、直线中,线段最短 |
20.要使$\sqrt{9+2x}$在实数范围内有意义,则( )
| A. | x为任何值 | B. | x≤-$\frac{9}{2}$ | C. | x≥$\frac{9}{2}$ | D. | x≥-$\frac{9}{2}$ |
7.三元一次方程组$\left\{\begin{array}{l}{2x-3y+2z=5}\\{x-2y+3z=-6}\\{3x-y+z=3}\end{array}\right.$ 消去未知数y后,得到的方程组可能是( )
| A. | $\left\{\begin{array}{l}{7x+z=4}\\{5x-z=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7x+z=4}\\{x-5z=8}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{7x-z=12}\\{x-5z=28}\\{\;}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x-z=4}\\{x-5z=12}\end{array}\right.$ |
4.201718的个位上的数字是( )
| A. | 7 | B. | 3 | C. | 9 | D. | 1 |
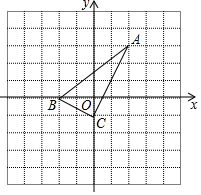 如图,直 角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)
如图,直 角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)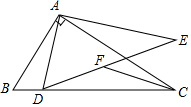 如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=6,AC=8,F为DE中点,若点D在直线BC上运动,连接CF,则在点D运动过程中,线段CF的最小值是4.
如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB=6,AC=8,F为DE中点,若点D在直线BC上运动,连接CF,则在点D运动过程中,线段CF的最小值是4.