题目内容
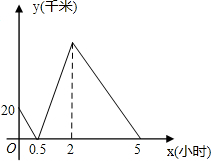在一条笔直的航道上有A、B、C三个港口，一艘轮船从A港出发，匀速航行到C港后返回到B港，轮船离B港的距离y（千米），与航行时间x（小时）之间的函数关系如图所示，若航行过程中水流速度和轮船的静水速度保持不变，则水流速度为考点：一次函数的应用
专题：
分析：设轮船在静水的速度为a千米/小时，水流速度为b千米/小时，根据图象求出从A到B时的速度a+b，再根据从B到C与从C到B的路程相同列出方程求出a-b，然后联立两方程求解即可．
解答：解：设轮船在静水的速度为a千米/小时，水流速度为b千米/小时，
在0到0.5小时时，从A到B，a+b=20÷0.5=40①，
在从B到C时与从C返回B时，（a+b）×（2-0.5）=（a-b）×（5-2），
整理得，a-b=20②，
联立
，
解得
，
所以，水流速度为10千米/小时．
故答案为：10．
在0到0.5小时时，从A到B，a+b=20÷0.5=40①，
在从B到C时与从C返回B时，（a+b）×（2-0.5）=（a-b）×（5-2），
整理得，a-b=20②，
联立
|
解得
|
所以，水流速度为10千米/小时．
故答案为：10．
点评：本题考查了一次函数的应用，主要利用了速度=路程÷时间的关系式，准确识图，理清轮船在A、B、C三个港口的运动过程是解题的关键．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
相关题目
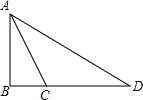如图，在△ABC中．∠B=90°，∠BAC=30°．AB=9cm，D是BC延长线上一点．且AC=DC．则
给出下列程序
，且当输入1时，输出值为3；输入0时，输出值为2．则当输入x值为-1时，输出值为（ ）
，且当输入1时，输出值为3；输入0时，输出值为2．则当输入x值为-1时，输出值为（ ）| A、1 | B、-1 | C、0 | D、2 |
车厘子就是英语单词cherries（樱桃）的音译，车厘子的含铁量特别高，位于各种水果之首，常食车厘子可补充体内对铁元素的需求，促进血红蛋白再生，既可防治缺铁性贫血．又可增强体质，健脑益智，车厘子营养丰富，具有调中益气，健脾和胃，祛风湿，“令人面孔好颜色”之功效，对食欲不振，消化不良，风湿身痛等等均有益处．2011年1月份至6月份重庆市某商场车厘子销售价格y（元）与月份x（1≤x≤6且x为整数）之间的函数关系式如下表：