题目内容
小明在学校运动会上负责联络,他先从检录处走了75米到达起点,又从起点向东走了100米到达终点,最后从终点走了125米回到检录处,则他开始是按 方向走的.
考点:勾股定理的逆定理
专题:
分析:先画出图形,用J、Q、Z分别表示检录处、起点、终点,则JQ=75米,QZ=100米,JZ=125米,由勾股定理的逆定理判定∠JQZ=90°,再由他从起点向东走了100米到达终点,得出他开始是按向南或向北方向走的.
解答: 解:如图,用J、Q、Z分别表示检录处、起点、终点,则JQ=75米,QZ=100米,JZ=125米,
解:如图,用J、Q、Z分别表示检录处、起点、终点,则JQ=75米,QZ=100米,JZ=125米,
∵752+1002=1252,
∴JQ2+QZ2=JZ2,
∴∠JQZ=90°,
∵从起点向东走了100米到达终点,
∴他从检录处向南或向北走了75米到达起点,即他开始是按向南或向北方向走的.
故答案为向南或向北.
 解:如图,用J、Q、Z分别表示检录处、起点、终点,则JQ=75米,QZ=100米,JZ=125米,
解:如图,用J、Q、Z分别表示检录处、起点、终点,则JQ=75米,QZ=100米,JZ=125米,∵752+1002=1252,
∴JQ2+QZ2=JZ2,
∴∠JQZ=90°,
∵从起点向东走了100米到达终点,
∴他从检录处向南或向北走了75米到达起点,即他开始是按向南或向北方向走的.
故答案为向南或向北.
点评:本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.准确画出图形是解题的关键.

练习册系列答案
相关题目
一元二次不等式ax2+bx+2>0的解为-
<x<
,则a-b=( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、10 | B、-14 |
| C、-10 | D、-8 |
点A(x1,y1)和B(x2,y2)都在直线y=-x上,且x1>x2,则y1与y2的关系是( )
| A、y1≥y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、y1>y2 |
约分
的结果是( )
| 2xy |
| -x2y |
| A、-1 | ||
| B、-2x | ||
C、-
| ||
D、
|
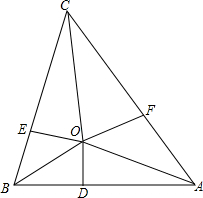 如图,已知在△ABC中,AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线,AB=4,BC=5,CA=6,OD⊥AB,OE⊥BC,OF⊥AC,求OD的长.
如图,已知在△ABC中,AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线,AB=4,BC=5,CA=6,OD⊥AB,OE⊥BC,OF⊥AC,求OD的长. 如图,△A′B′C′是将△ABC放大后的图形,若图中线段AA′=
如图,△A′B′C′是将△ABC放大后的图形,若图中线段AA′=