题目内容
一个均匀的立方体骰子的六个面上标有数1，2，3，4，5，6，随机地掷两次骰子，那么第二次得到的数字大于第一次得到的数字的概率是多少？
解：根据题意，列出如下的表格
从表格可以看出，所有可能出现的结果共有36个．
第二次得到的数字大于第一次得到的数字（记为事件A）的结果有15个，即（1，2），（1，3），（1，4），（1，5），（1，6），（2，3），（2，4），（2，5），（2，6），（3，4），（3，5），（3，6），（4，5），（4，6），（5，6），那么P（A）=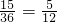
．
分析：列举出所有情况，看所求的情况占总情况的多少即可．
点评：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
，注意本题是放回实验．
| 后 先 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| 5 | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| 6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
第二次得到的数字大于第一次得到的数字（记为事件A）的结果有15个，即（1，2），（1，3），（1，4），（1，5），（1，6），（2，3），（2，4），（2，5），（2，6），（3，4），（3，5），（3，6），（4，5），（4，6），（5，6），那么P（A）=
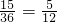．分析：列举出所有情况，看所求的情况占总情况的多少即可．
点评：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
，注意本题是放回实验． 
练习册系列答案
阅读快车系列答案
相关题目