题目内容
20.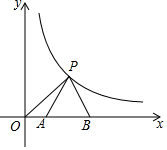 如图,P(m,m)是反比例函数y=$\frac{9}{x}$在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )
如图,P(m,m)是反比例函数y=$\frac{9}{x}$在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )| A. | $\frac{9}{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{9+12\sqrt{3}}{4}$ | D. | $\frac{9+3\sqrt{3}}{2}$ |
分析 易求得点P的坐标,即可求得点B坐标,即可解题.
解答 解:作PD⊥OB,
∵P(m,m)是反比例函数y=$\frac{9}{x}$在第一象限内的图象上一点,
∴m=$\frac{9}{m}$,解得:m=3,
∴PD=3,
∵△ABP是等边三角形,
∴BD=$\frac{\sqrt{3}}{3}$PD=$\sqrt{3}$,
∴S△POB=$\frac{1}{2}$OB•PD=$\frac{1}{2}$(OD+BD)•PD=$\frac{9+3\sqrt{3}}{2}$,
故选 D.
点评 本题考查了等边三角形的性质,考查了反比例函数点坐标的特性,本题中求得m的值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.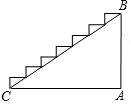 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )| A. | 3.5sin29°米 | B. | 3.5cos29°米 | C. | 3.5tan29°米 | D. | $\frac{3.5}{cos29°}$米 |
15. 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )| A. | 传 | B. | 统 | C. | 文 | D. | 化 |
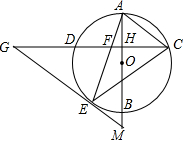 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过$\widehat{BD}$上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.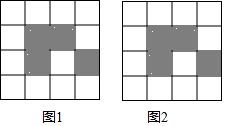 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.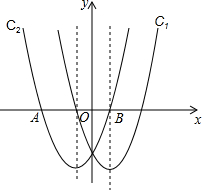 在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.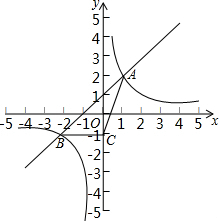 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.