题目内容
1.若样本x1,x2,…,xn的平均数为$\overline{x}$=5,方差S2=0.025,则样本x1+3,x2+3,…,xn+3的平均数$\overline{x}$′和方差S’2分别为8和0.025.分析 根据平均数和方差的变化规律,当数据都加上一个数(或减去一个数)时,方差不变,平均数相应的加上或减去这个数,即可得出答案.
解答 解:∵样本x1,x2,…,xn的平均数为5,
∴样本x1+3,x2+3,…,xn+3的平均数是5+3=8;
∵样本x1,x2,…,xn的方差为0.025,
∴样本x1+3,x2+3,…,xn+3的方差是0.025;
故答案为:8,0.025.
点评 本题考查方差、平均数的意义,关键是找出新样本的平均数和方差与原样本的平均数和方差之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在8点30分时,时针上的时针与分针之间的夹角为( )
| A. | 85度 | B. | 75度 | C. | 70度 | D. | 60度 |
10.甲、乙两人相距50千米,若同向而行,乙10小时可追上甲;若相向而行,2小时两人相遇.设甲、乙两人每小时分别走x千米、y千米,则可列出方程组是( )
| A. | $\left\{\begin{array}{l}{10x-10y=50}\\{2x+2y=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{10x+10y=50}\\{2x+2y=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{10y-10x=50}\\{2x+2y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{10x-10y=50}\\{2x-2y=50}\end{array}\right.$ |
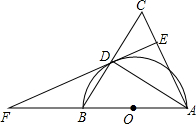 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.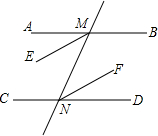 如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF.
如图,已知直线AB∥CD,直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF.