Question

【题目】如图①，点为直线上一点，过点作射线，使，将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的上方.

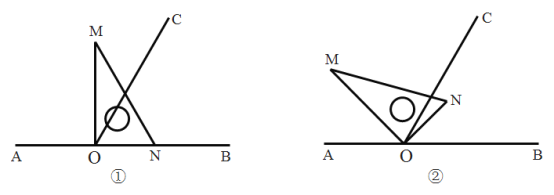
（1）在图①中，__________度；

（2）将图①中的三角板绕点按逆时针方向旋转，使得在的内部，如图②，若，求的度数；

（3）将图①中的三角板绕点以每秒的速度沿逆时针方向旋转一周，在旋转的过程中，当直线恰好平分锐角时，旋转的时间是__________秒.（直接写出结果）

Answer 1

【答案】（1）30；（2）54°；（3）3或21.

【解析】

（1）由题意得出∠MON=90°，得出∠COM=∠MON-∠BOC=90°-60°=30°；

（2）设∠BON=α，则∠NOC=60°-α，∠MOC=∠MON-∠NOC=90°-60°+α=30°+α，∠MOA=180°-∠MON-∠BON=180°-90°-α=90°-α，由题意得出60°-α=（90°-α），解得α=54°即可；

（3）求出∠BON=30°或∠BON=210°，即可得出答案．

（1）∵将一直角三角板的直角顶点放在点O处，一边ON在射线OB上，另一边OM在直线AB的上方，

∴∠MON=90°，

∴∠COM=∠MON-∠BOC=90°-60°=30°，

（2）设∠BON=α，

∵∠BOC=60°，

∴∠NOC=60°-α，

∵∠MON=90°，

∴∠MOC=∠MON-∠NOC=90°-60°+α=30°+α，

∠MOA=180°-∠MON-∠BON=180°-90°-α=90°-α，

∵∠NOC=∠MOA，

∴60°-α=（90°-α），

解得：α=54°，

即∠BON=54°；

（3）∵直线ON平分∠BOC，∠BOC=60°，

∴∠BON=30°或∠BON=210°，

∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周，

∴直线ON平分∠BOC时，旋转的时间是3或21秒，

故答案为：3或21.