题目内容
12.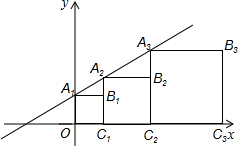 在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是(15,8),点Bn的坐标是(2n-1,2n-1).
在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是(15,8),点Bn的坐标是(2n-1,2n-1).
分析 根据一次函数,得出A1、A2等点的坐标,继而得知B1、B2A等点的坐标,从中找出规律,进而可求出第n个B点的坐标.
解答 解:把x=0代入直线y=x+1,可得:y=1,
所以可得:点B1的坐标是(1,1)
把x=1代入直线y=x+1,可得:y=2,
所以可得:点B2的坐标是(3,2),
同理可得点B3的坐标是(7,4);点B4的坐标是(15,8);
由以上得出规律是Bn的坐标为(2n-1,2n-1).
故答案为:(15,8);(2n-1,2n-1).
点评 本题考查了正方形的性质,解此题的关键是根据一次函数的点的坐标计算的结果得出规律,题目比较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目
3. 如图,是一个工件的三视图,则此工件的全面积是( )
如图,是一个工件的三视图,则此工件的全面积是( )
 如图,是一个工件的三视图,则此工件的全面积是( )
如图,是一个工件的三视图,则此工件的全面积是( )| A. | 85πcm2 | B. | 90πcm2 | C. | 155πcm2 | D. | 165πcm2 |
20.2015年元旦期间,北京各大公园接待游客达245 000万人次.其中,“冰雪乐园”吸引了大批游客亲身感受冰雪带来的快乐,一起为北京申办2022年冬奥会助力加油.用科学记数法表示245 000,正确的是( )
| A. | 24.5×104 | B. | 2.45×105 | C. | 2.45×106 | D. | 0.245×106 |
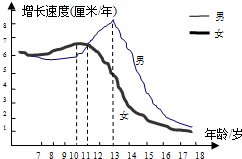 生物学研究表明在8-17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是13岁,在11岁时男生女生的身高增长速度是一样的.
生物学研究表明在8-17岁期间,男女生身高增长速度规律呈现如图所示,请你观察此图,回答下列问题:男生身高增长速度的巅峰期是13岁,在11岁时男生女生的身高增长速度是一样的.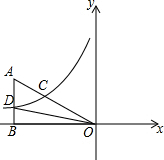 在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,连接AO.双曲线$y=\frac{k}{x}$经过斜边AO的中点C,与边AB交于点D.
在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,连接AO.双曲线$y=\frac{k}{x}$经过斜边AO的中点C,与边AB交于点D.