题目内容
17.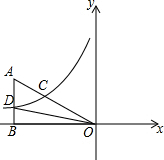 在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,连接AO.双曲线$y=\frac{k}{x}$经过斜边AO的中点C,与边AB交于点D.
在平面直角坐标系xOy中,过点A(-4,2)向x轴作垂线,垂足为B,连接AO.双曲线$y=\frac{k}{x}$经过斜边AO的中点C,与边AB交于点D.(1)求反比例函数的解析式;
(2)求△BOD的面积.
分析 (1)设所求反比例函数的解析式为y=$\frac{k}{x}$,先根据中点坐标公式求出点C的坐标,再将点C坐标代入y=$\frac{k}{x}$,利用待定系数法即可求解;
(2)根据反比例函数比例系数k的几何意义即可求解.
解答 解:(1)设所求反比例函数的解析式为y=$\frac{k}{x}$,
∵A(-4,2),AO的中点为C,
∴C(-2,1).
∵双曲线$y=\frac{k}{x}$经过点C,
∴k=-2×1=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$;
(2)∵反比例函数y=-$\frac{2}{x}$经过点D,DB⊥x轴于B,
∴S△BOD=$\frac{1}{2}$×|k|=$\frac{1}{2}$×2=1.
点评 本题考查了待定系数法求反比例函数的解析式,中点坐标公式,反比例函数比例系数k的几何意义,都是中学阶段的重点内容,需熟练掌握.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
7.若点M(x,y)满足x+y=0,则点M位于( )
| A. | 第一、三象限两坐标轴夹角的平分线上 | |
| B. | x轴上 | |
| C. | 第二、四象限两坐标轴夹角的平分线上 | |
| D. | y轴上 |
5.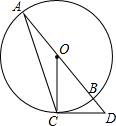 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,连接OC,AC.若∠D=50°,则∠A的度数是( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
2.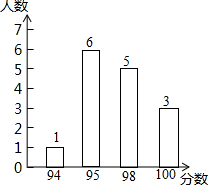 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
 某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )
某次比赛中,15名选手的成绩如图所示,则这15名选手成绩的众数和中位数分别是( )| A. | 98,95 | B. | 98,98 | C. | 95,98 | D. | 95,95 |
9.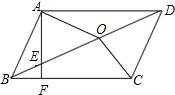 如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
 如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 如图,△AED∽△ACB,△AED的面积为△ACB面积的$\frac{1}{3}$,则AD:AB=$\sqrt{3}$:3.
如图,△AED∽△ACB,△AED的面积为△ACB面积的$\frac{1}{3}$,则AD:AB=$\sqrt{3}$:3.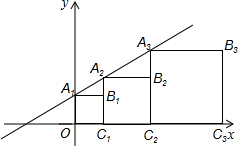 在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是(15,8),点Bn的坐标是(2n-1,2n-1).
在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是(15,8),点Bn的坐标是(2n-1,2n-1).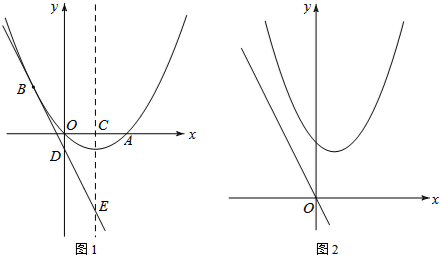
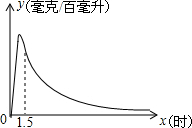 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).