题目内容
若x+ =2,则x2+
=2,则x2+ =________,x3+
=________,x3+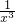 =________,x4+
=________,x4+ =________.任意正整数n,猜想:
=________.任意正整数n,猜想: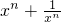 =________.
=________.
2 2 2 2
分析:先根据x+ =2求出(x+
=2求出(x+ )2=4,进而可得出x2+
)2=4,进而可得出x2+ 的值,同理求出x3+
的值,同理求出x3+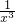 及x4+
及x4+ 的值,找出规律即可进行解答.
的值,找出规律即可进行解答.
解答:∵x+ =2,
=2,
∴(x+ )2=4,
)2=4,
∴x2+ =2;
=2;
∵x3+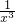 =(x+
=(x+ )(x2+
)(x2+ -1),
-1),
=2×(2-1),
=2;
x4+ =(x2+
=(x2+ )2-2,
)2-2,
=4-2,
=2,
…
故xn+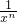 =2.
=2.
故答案为:2.
点评:本题考查的是完全平方公式及立方和公式,能根据题意得出x2+ =2是解答此题的关键.
=2是解答此题的关键.
分析:先根据x+
 =2求出(x+
=2求出(x+ )2=4,进而可得出x2+
)2=4,进而可得出x2+ 的值,同理求出x3+
的值,同理求出x3+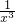 及x4+
及x4+ 的值,找出规律即可进行解答.
的值,找出规律即可进行解答.解答:∵x+
 =2,
=2,∴(x+
 )2=4,
)2=4,∴x2+
 =2;
=2;∵x3+
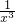 =(x+
=(x+ )(x2+
)(x2+ -1),
-1),=2×(2-1),
=2;
x4+
 =(x2+
=(x2+ )2-2,
)2-2,=4-2,
=2,
…
故xn+
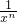 =2.
=2.故答案为:2.
点评:本题考查的是完全平方公式及立方和公式,能根据题意得出x2+
 =2是解答此题的关键.
=2是解答此题的关键. 
练习册系列答案
相关题目
下列结论错误的是( )
| A、若a=b,则a-c=b-c | ||||
B、若a=b,则
| ||||
| C、若x=2,则x2=2x | ||||
| D、若ax=bx,则a=b |